Os modelos de Redes Neurais conhecidos como Transformers têm provavelmente a arquitetura mais discutida no momento. Para entender como os Transformers funcionam, precisamos primeiramente entender o mecanismo de Atenção (Attention Mechanism), apresentado pelo Google em 2017 no artigo Attention is All You Need.
Em nosso post anterior, Visualizando um Modelo de Tradução (Seq2seq com Attention), nós demos maior atenção ao mecanismo de Atenção em si. Este conceito que melhorou, inicialmente, o desempenho das Redes Neurais em aplicações de tradução.
Agora, neste post, iremos conversar sobre a arquitetura de Transformers. Uma arquitetura que usa a Atenção para acelerar a velocidade em que os modelos de linguagem podem ser treinados. O maior benefício vem do fato que os Transformers fazem uso da paralelização no seu processo de treino. Inclusive, a recomendação da Google Cloud é de usar Transformers como modelo de referência para a sua oferta de Cloud TPU. Portanto, vamos tentar desmembrar o modelo e analisar como ele funciona.
Uma implementação em código com TensorFlow dos Transformers está disponível como parte do pacote Tensor2Tensor. O grupo de NLP (Natural Language Processing, ou Processamento de Linguagem Natural) de Harvard criou um guia anotado do artigo com implementação em PyTorch.
Neste post, originalmente chamado de The Illustrated Transformer, o autor, Jay Alammar, tenta simplificar os conceitos e apresentá-los um de cada vez. O objetivo é facilitar o entendimento para pessoas sem o conhecimento profundo de Deep Learning.
O Jay Alammar é especialista em Processamento de Linguagem Natural. Escreveu alguns artigos super didáticos no seu blog (https://jalammar.github.io/). Com a sua autorização, estamos trazendo alguns deles para o BRAINS, em Português.
Obs: Todo o texto abaixo foi traduzido do conteúdo original, exceto as notas de tradução explicitadas.
Um olhar de alto nível
Vamos começar olhando para o modelo como uma caixa preta. Em uma aplicação de tradução, o modelo receberia uma frase em um idioma e retornaria a sua tradução em outro. No caso aqui, “Eu sou um estudante” seria traduzido do francês (“Je suis étudiant”) para o inglês (“I am a student”).

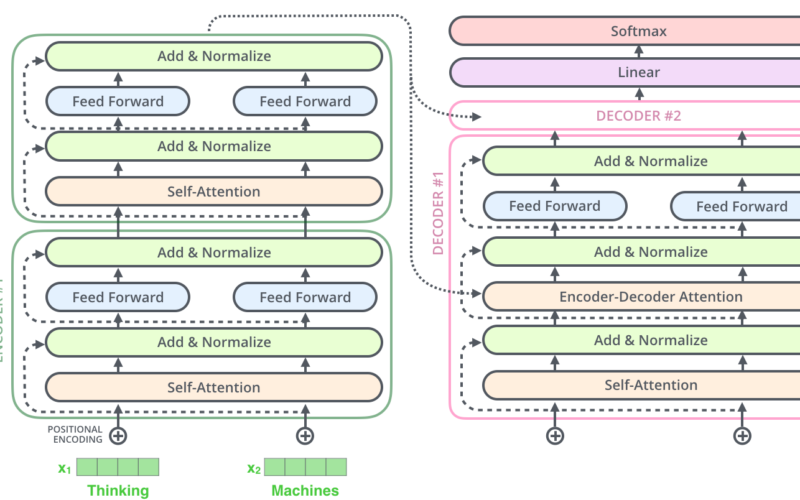
Abrindo o capô dessa maravilha do Optimus Prime, podemos ver componentes de codificação (Encoders), componentes de decodificação (Decoders) e conexões entre eles.
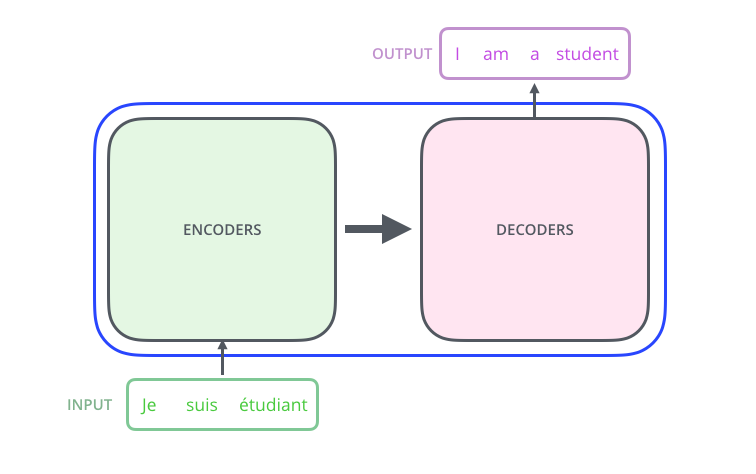
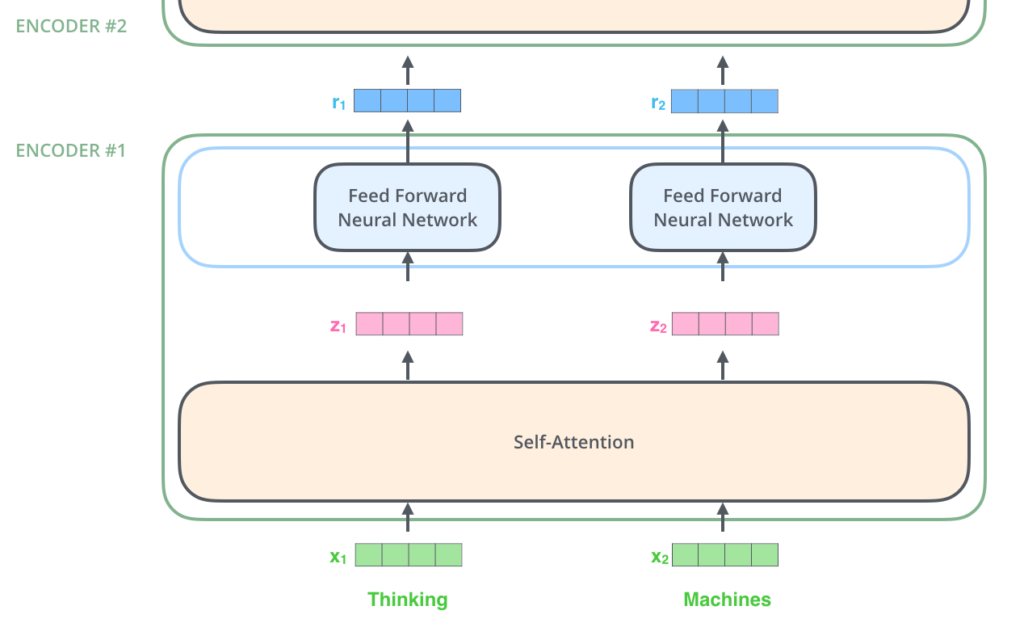
O componente de codificação é uma pilha de Encoders (o artigo original empilha seis deles, uns sobre os outros – não há nada de mágico com o número seis, nós podemos sem dúvidas fazer experimentos com outras quantidades). O componente de decodificação é uma pilha de Decoders do mesmo número.

Os Encoders são todos idênticos em estrutura (ainda que não compartilhem os pesos, ou Weights, como rede neural). Cada um é quebrado em duas subcamadas:
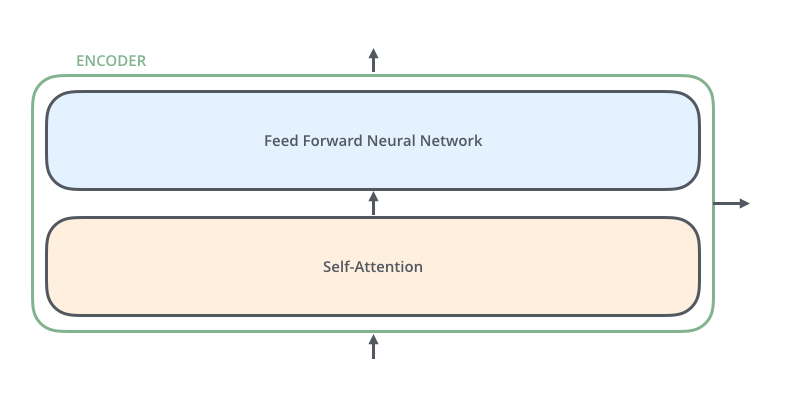
As entradas do Encoder passam primeiro por uma camada de Self-Attention, ou “Auto Atenção” – uma camada que ajuda o Encoder a examinar as outras palavras na frase enquanto codifica uma palavra específica. Vamos analisar de perto a Self-Attention mais à frente neste post.
As saídas da camada de Self-Attention são alimentadas em uma Rede Neural de Feed Forward, ou “Alimentação Direta”. Exatamente a mesma Feed Forward Neural Network é aplicada independentemente, a cada posição.
O Decoder possui estas duas camadas, mas entre elas, há uma camada de Encoder-Decoder Attention. Esta ajuda o Decoder a focar nas partes mais relevantes da frase de entrada (semelhante ao que a Atenção faz em modelos de sequência para sequência – seq2seq).
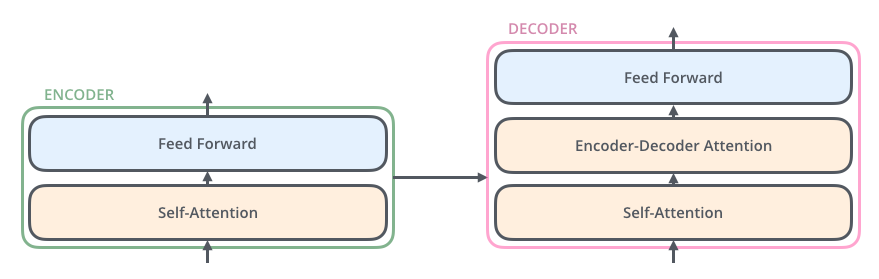
Trazendo os Tensores à cena
Agora que vimos os principais componentes do modelo de Transformers, vamos começar a observar os vários vetores/tensores e como eles fluem entre esses componentes para transformar a entrada de um modelo treinado em uma saída que faça sentido.
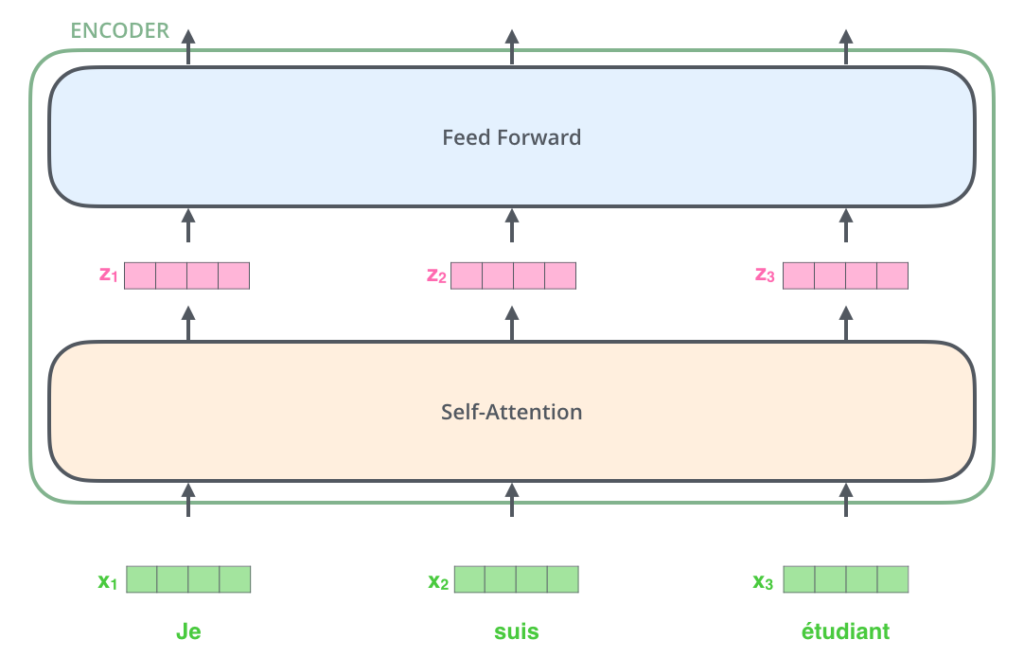
Como é o caso em aplicações de Processamento de Linguagem Natural (Natural Language Processing, ou NLP) em geral, começamos convertendo cada palavra de entrada em um vetor usando um algoritmo de Embedding.

Os Embeddings são gerados apenas no primeiro Encoder, o mais inferior. A abstração comum a todos os Encoders é que eles recebem uma lista de vetores, cada um com tamanho 512. No primeiro Encoder, esses vetores seriam os Embeddings das palavras, mas nos outros Encoders, seriam as saídas do Encoder diretamente abaixo. O tamanho desta lista é um hiperparâmetro que podemos definir: basicamente, seria o comprimento da frase mais longa em nosso conjunto de dados de treino.
Após a geração dos Embeddings das palavras na nossa sequência de entrada, cada uma delas passa por cada uma das camadas de Encoder.
Aqui nós começamos a ver uma propriedade fundamental dos Transformers, que é que a palavra em cada posição flui pelo seu próprio caminho no Encoder. Existem dependências entre esses caminhos na camada de Self-Attention. No entanto, a camada de Feed-Forward não possui estas dependências, e assim os vários caminhos podem ser executados em paralelo enquanto fluem pela camada de Feed-Forward.
A seguir, vamos mudar o exemplo para uma frase mais curta. Iremos examinar o que acontece em cada subcamada do Encoder.
Agora nós estamos fazendo Encoding!
Como já mencionamos anteriormente, o componente de codificação, o Encoder, recebe uma lista de vetores como entrada. O Encoder processa esta lista passando esses vetores pela camada de Self-Attention. Depois, passa pela Rede Neural Feed-Forward. Só então envia a saída para cima, para o próximo Encoder.
Self-Attention em um alto nível
Não se deixe enganar pelo fato de estarmos distribuindo o termo “Self-Attention” como se fosse um conceito que todo mundo devesse conhecer. Eu mesmo, pessoalmente, nunca tinha me deparado com este conceito até ler o artigo Attention is All You Need. Vamos simplificar como isso funciona.
Vamos supor que temos a seguinte frase como entrada e queremos traduzi-la:
The animal didn't cross the street because it was too tired.
Mas a palavra “it” nesta frase se refere ao que? Está se referindo à rua ou ao animal? A rua estava cansada? Ou o animal estava cansado? É uma pergunta simples para um humano. Mas não tão simples para um algoritmo.
Quando o modelo está processando a palavra “it”, a Self-Attention permite associar “it” com “animal”.
Conforme o modelo processa cada palavra (cada posição na sequência de entrada), a Self-Attention permite que ele olhe para outras posições da sequência de entrada em busca de pistas que possam ajudar a entender melhor esta palavra. Assim conseguimos um melhor Encoding da palavra.
Se você está familiarizado com as Redes Neurais Recorrentes (RNNs), pense em como a manter um Hidden State, um Estado Oculto, permite que a RNN incorpore sua representação de palavras/vetores anteriores que já processou com a palavra atual que está processando. A Self-Attention é o método que os Transformers usam para incorporar o “entendimento” de outras palavras relevantes na palavra que estamos processando no momento.

Não deixe de conferir o notebook Tensor2Tensor, onde você pode carregar um modelo de Transformers e examiná-lo usando uma visualização interativa.
Self-Attention em detalhes
Vamos primeiro ver como calcular a Self-Attention usando vetores. Então iremos continuar para ver como de fato é implementada – usando matrizes.
O primeiro passo para calcular a Self-Attention é criar três vetores a partir de cada vetor de entrada do Encoder. Neste caso, o Embedding de cada palavra. Então para cada palavra, nós criamos um vetor Query, um vetor Key, e um vetor Value. Estes vetores são criados multiplicando os Embeddings por três matrizes que foram aprendidas durante o processo de treino.
Note que estes novos vetores são menores em dimensões que o vetor de Embeddings. A dimensionalidade é de 64. Os vetores de Embeddings e os de entrada/saída do Encoder têm dimensionalidade de 512. Eles não PRECISAM ser menores, esta é uma escolha de arquitetura para tornar o cálculo de Multiheaded Attention (em grande parte) constante.

O que são os vetores Query, Key e Value?
Eles são abstrações que são úteis para calcular e pensar sobre Atenção. Uma vez que você siga com a leitura sobre como a Atenção é calculada abaixo, você vai saber praticamente tudo que precisa saber sobre os papéis que cada um desses vetores desempenha.
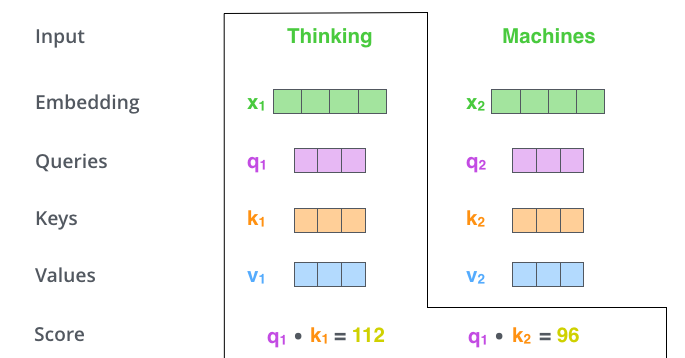
O segundo passo para calcular a Self-Attention é calcular um escore. Digamos que estamos calculando a Self-Attention para a primeira palavra deste exemplo, “Thinking”. Precisamos atribuir um escore para cada palavra da frase de entrada em relação a esta palavra. O escore determina o quanto devemos focar em outras partes da frase enquanto codificamos uma palavra em uma determinada posição.
O escore é calculado tomando o produto escalar do vetor Query com o vetor Key da respectiva palavra que estamos atribuindo o escore. Portanto, se estamos processando a Self-Attention para a palavra na posição #1, o primeiro escore seria o produto escalar de q1 com k1. O segundo escore seria o produto escalar de q1 com k2.
O terceiro e quarto passos são dividir os escores por 8. Dividimos pela raiz quadrada das dimensões dos vetores usados no artigo – 64. Isso nos leva a ter gradientes mais estáveis. Poderíamos ter outros valores possíveis aqui, mas este é o padrão. Após isso, passamos o resultado por uma operação Softmax. A função Softmax normaliza os escores para que todos sejam positivos e se somem totalizando 1.
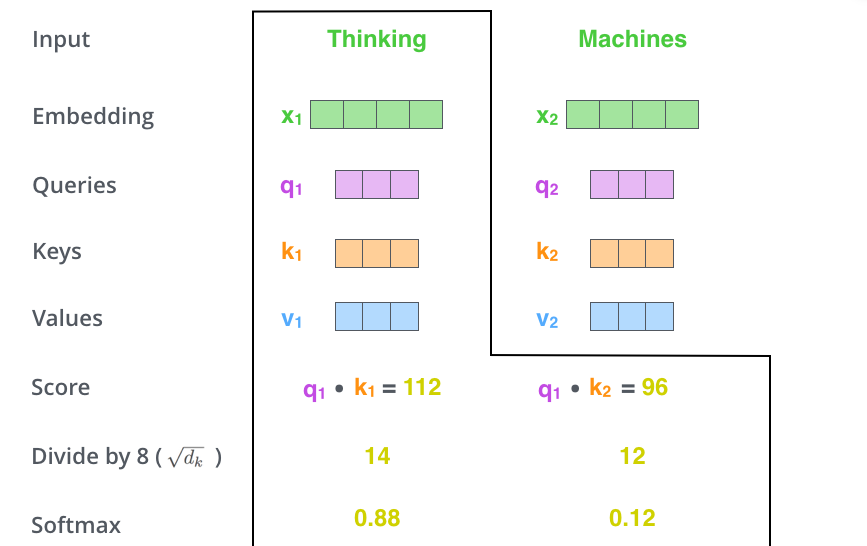
Este escore da Softmax determina o quanto cada palavra é expressiva nesta posição. Claramente a palavra nesta posição tem o maior escore de Softmax. Mas, às vezes, é útil se atentar a outra palavra que seja relevante para a palavra atual.
O quinto passo é multiplicar cada vetor de Value pelo escore de Softmax (em preparação para somá-los). A ideia aqui é manter intactos os valores da(s) palavra(s) que queremos focar, e diminuir a importância das palavras irrelevantes (multiplicando-as por números muito pequenos, como 0.001 por exemplo).
O sexto passo é somar os vetores de Value ponderados resultantes. Isso produz a saída da camada de Self-Attention nesta posição (para a primeira palavra).

Isso conclui o cálculo de Self-Attention. O vetor resultante é um que podemos enviar para a rede neural Feed-Forward. Na implementação real, entretanto, esse cálculo é feito em forma de matrizes para um processamento mais rápido. Então vamos ver como isso funciona agora, já que tivemos uma introdução sobre o cálculo a um nível de palavras.
Cálculo de matrizes da Self-Attention
O primeiro passo é calcular as matrizes Query, Key e Value. Nós fazemos isso empilhando nossos Embeddings em uma matriz X e multiplicando ela pelas matrizes que treinamos: WQ, WK e WV.

Finalmente, dado que estamos lidando com matrizes, nós podemos condensar os passos dois ao seis em uma fórmula para calcular a saída da camada de Self-Attention.
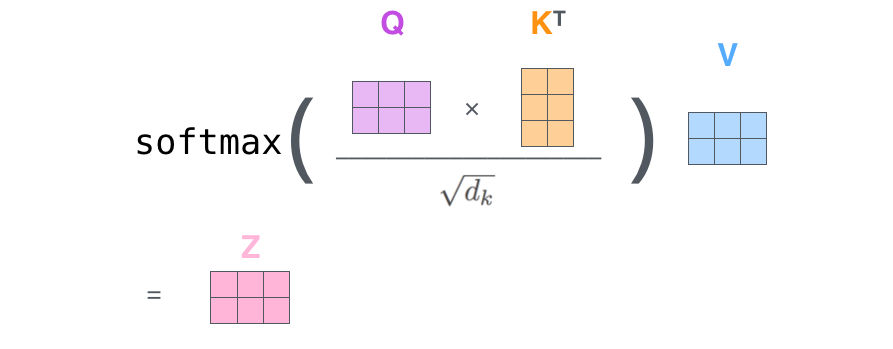
Um monstro de várias cabeças
O artigo refinou ainda mais a camada de Self-Attention adicionando um mecanismo chamado “Multi-Headed” Attention. Isso melhora o desempenho da camada de Atenção de duas maneiras:
- Expande a habilidade do modelo de forcar em diferentes posições. Sim, no exemplo acima, z1 contém um pouco de todos os outros Encodings, mas ele pode ser denominado a própria palavra mesmo. Se nós estamos traduzindo uma frase como “The animal didn’t cross the street because it was too tired”, seria útil saber a qual outra palavra “it” se refere.
- Dá à camada de Atenção múltiplos “subespaços de representação”. Como veremos a seguir, com a “Atenção Multi-Head” não temos apenas uma, mas várias matrizes de pesos de Query/Key/Value (os Transformers usam 8 “cabeças” de Atenção, então acabamos tendo 8 conjuntos para cada Encoder/Decoder). Cada um destes conjuntos é inicializado aleatoriamente. Então, depois do treino, cada conjunto é usado para projetar os Embeddings de entrada (ou vetores dos Encoders/Decoders inferiores) em um subespaço representativo diferente.
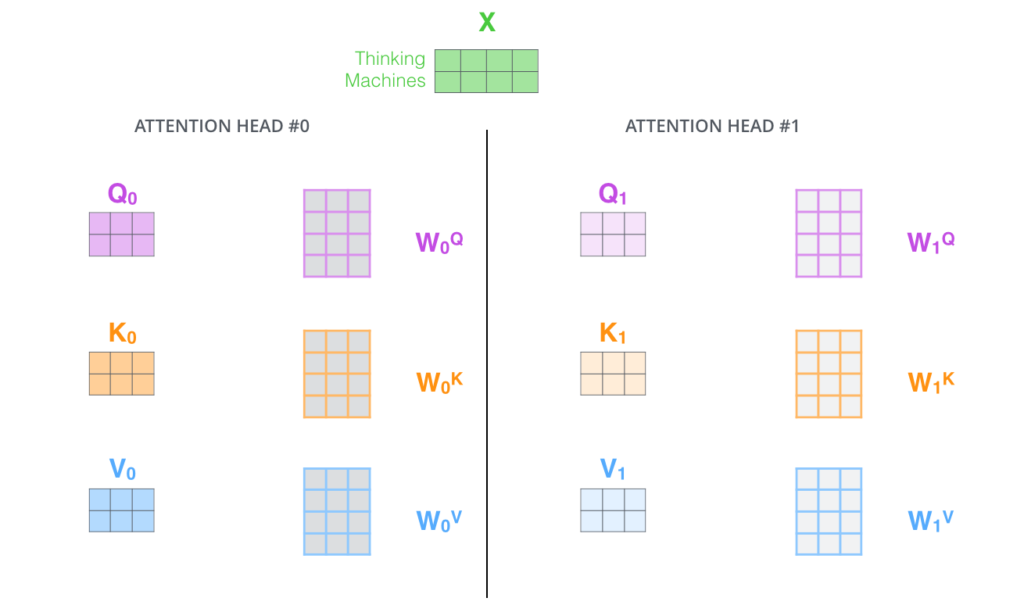
Se nós fizermos os mesmos cálculos de Self-Attention que destacamos acima, só que oito vezes diferentes com diferentes matrizes de pesos, nós acabamos com oito matrizes Z diferentes.
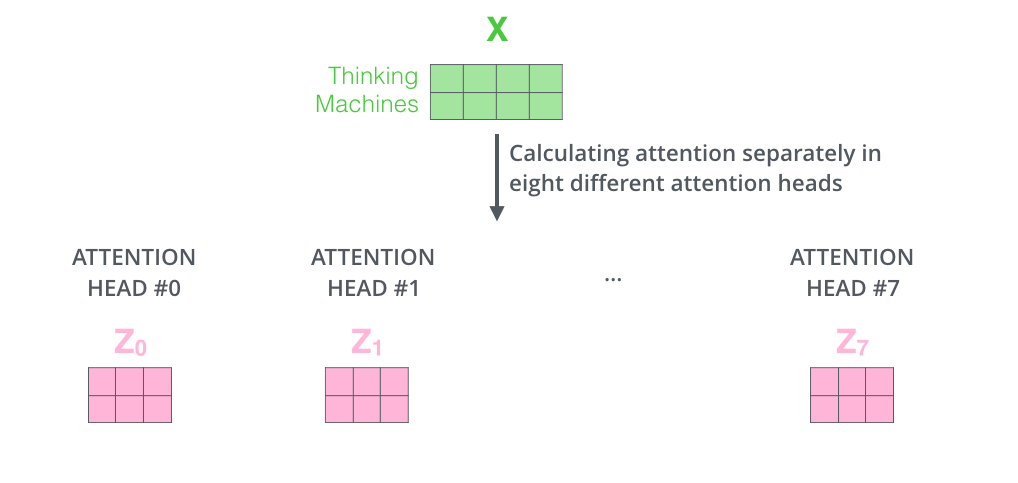
Isso nos deixa com um desafio. A camada de Feed-Forward não está esperando 8 matrizes. Está esperando uma única matriz (um vetor para cada palavra). Então nós precisamos de uma forma para condensar estas oito matrizes em uma única.
Como fazemos isso? Nós concatenamos as matrizes e então multiplicamos elas por uma matriz de pesos adicional WO.
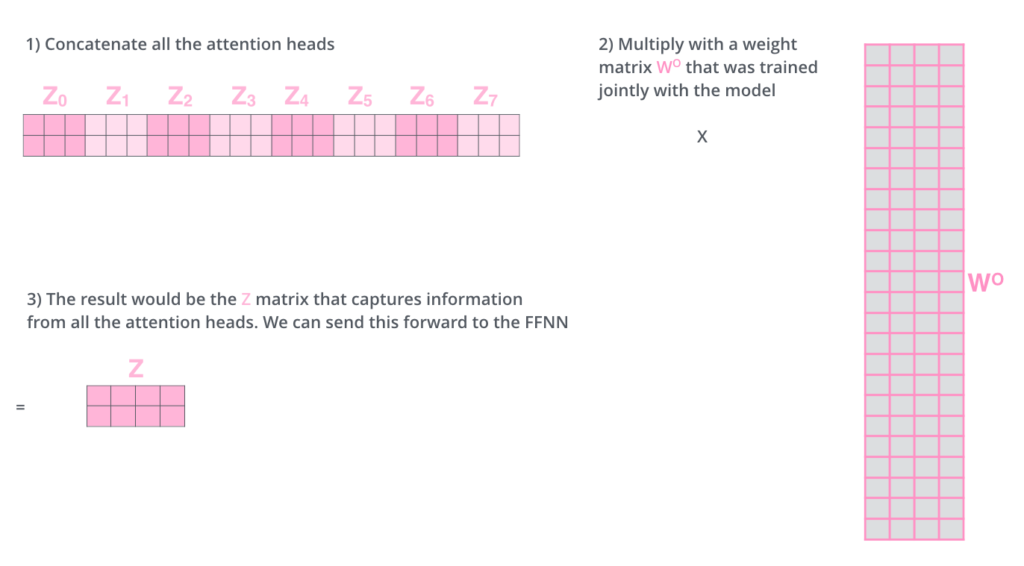
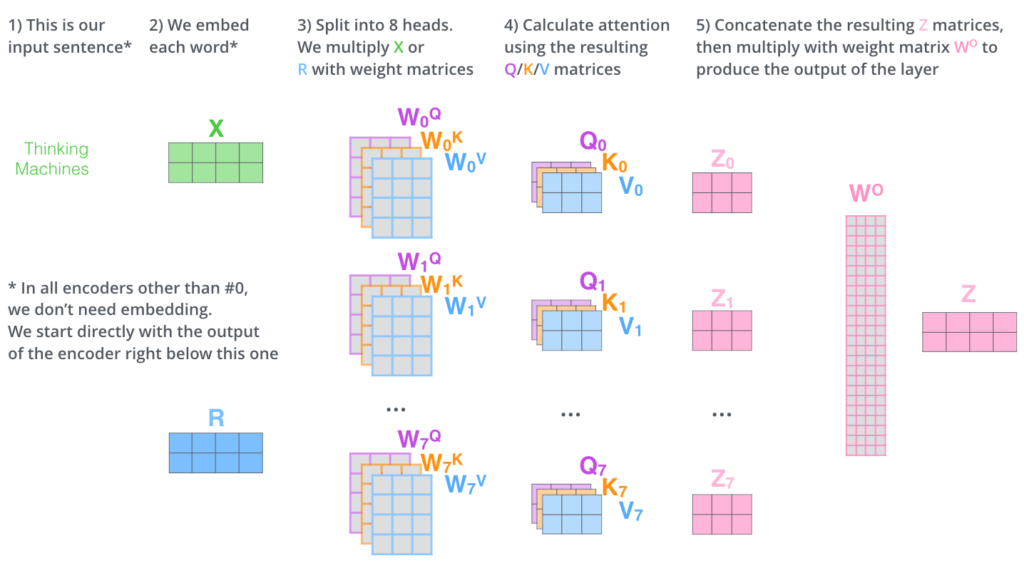
Isso é basicamente tudo que temos sobre a Multi-Headed Self-Attention. É um tanto de matrizes, eu reconheço. Nos permita tentar colocar todas elas de uma forma visual para podemos ver todas em um único lugar.
Agora que comentamos sobre as Attention Heads, vamos revisitar nosso exemplo de antes para ver como as diferentes heads da Atenção estão focando quando fazemos o Encoding da palavra “it” na nossa frase de exemplo.

Se adicionarmos todas as Attention Heads na figura, entretanto, as coisas começam a ficar mais difíceis de se entender.

Representando a ordem da sequência usando Encoding Posicional
Uma parte que está faltando do modelo como descrevemos até então é uma forma de levar em consideração a ordem das palavras da sequência de entrada.
Para endereçar isso, os Transformers adicionam mais um vetor a cada Embedding de entrada. Estes vetores seguem um padrão específico que o modelo aprende, que ajuda a determinar a posição de cada palavra, ou a distância entre diferentes palavras na frase. A ideia aqui é que adicionando estes valores aos Embeddings temos distâncias significativas entre os vetores de Embeddings quando são projetados em vetores Q/K/V durante o produto escalar da Atenção.
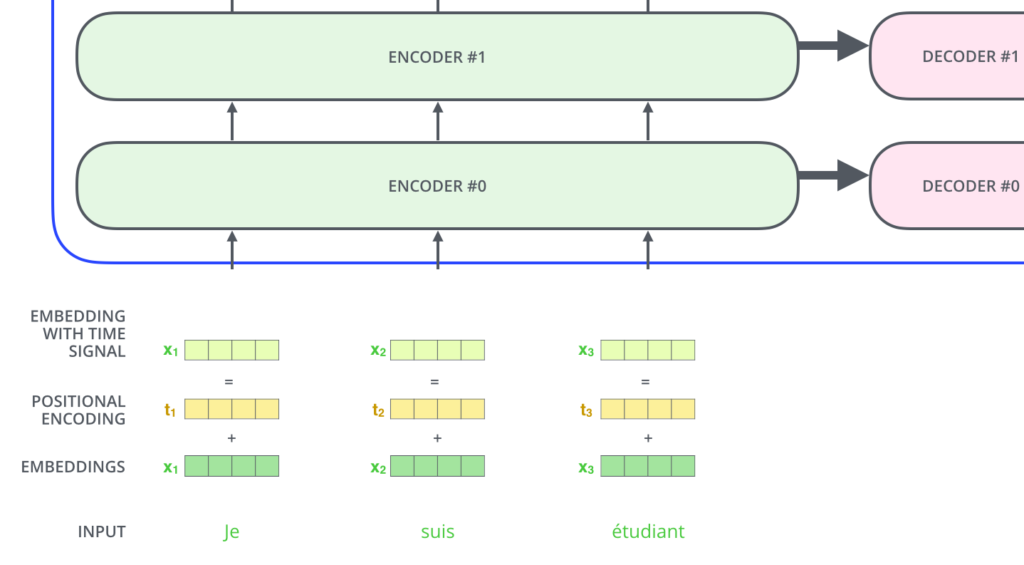
Se assumimos que os Embeddings têm uma dimensionalidade de 4, os Positional Encodings, ou Encodings Posicionais, se pareceriam com isso:
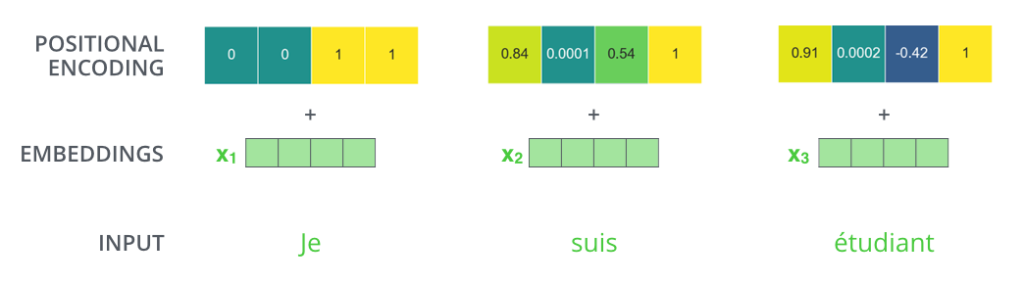
Na figura a seguir, cada linha corresponde a um Encoding Posicional de um vetor. Então a primeira linha seria o vetor que adicionaríamos ao Embedding da primeira palavra da frase de entrada. Cada linha contém 512 valores – cada um com um valor entre -1 e 1. Nós fizemos um código de cores para ficar fácil de visualizar o padrão.
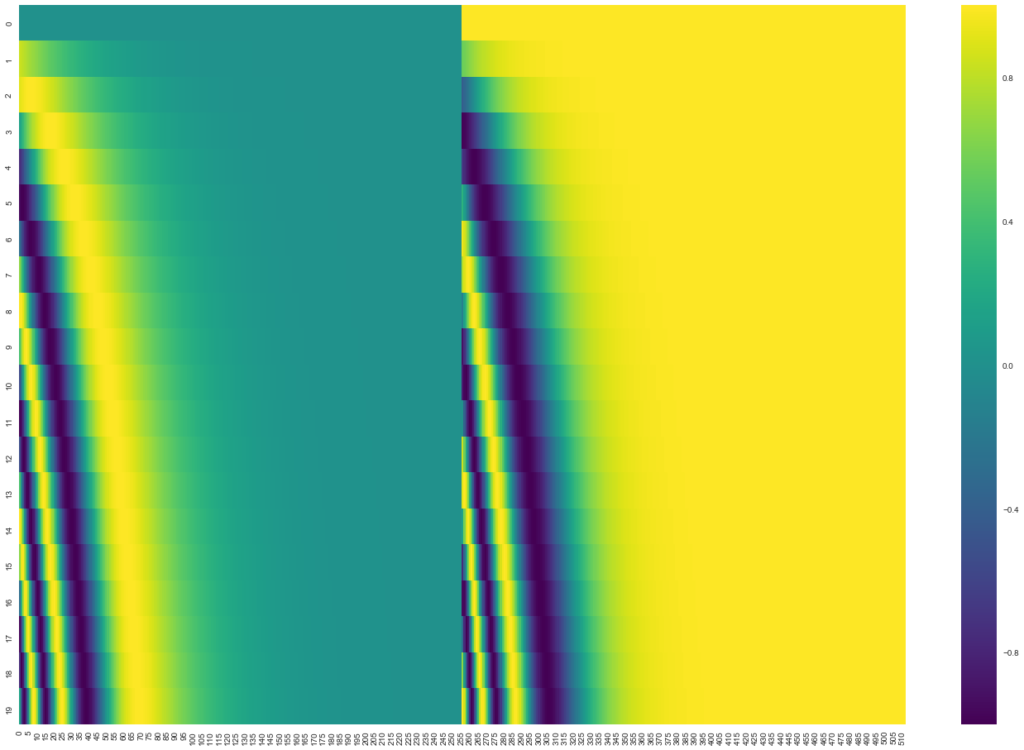
A fórmula para o Encoding Posicional é descrita no artigo (seção 3.5). Nós podemos ver o código para gerá-los no método get_timing_signal_1d(). Este não é o único método para Encoding Posicional. Entretanto, ele dá uma vantagem de poder escalar e generalizar para comprimentos de sequência nunca vistos (por exemplo se o nosso modelo treinado é pedido para traduzir uma frase mais longa do que qualquer outra na base de treino).
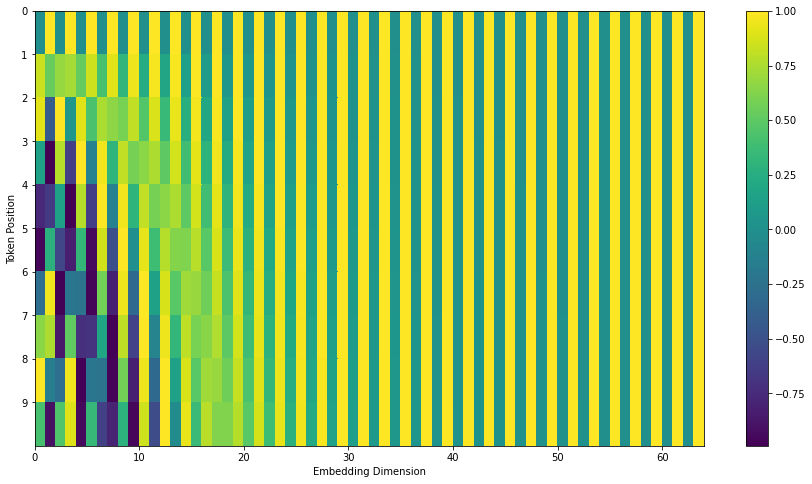
Atualização de Julho de 2020: O Encoding Posicional exibido acima é da implementação de Transformers do Tensor2Tensor. O método demonstrado no artigo é um pouco diferente e não concatena, mas intercala os dois sinais. A seguinte figura mostra como isso se parece. E aqui está o código para gerá-la.
Os Residuais
Um detalhe na arquitetura do Encoder que nós temos que mencionar antes de seguir em frente, é que em cada subcamada (Self-Attention, Feed-Forward) em cada Encoder tem uma conexão residual ao seu redor, e é seguida por um passo de normalização da camada.

Se nós visualizássemos os vetores e a operação de normalização de camada associada com a Self-Attention, se pareceria com isso:
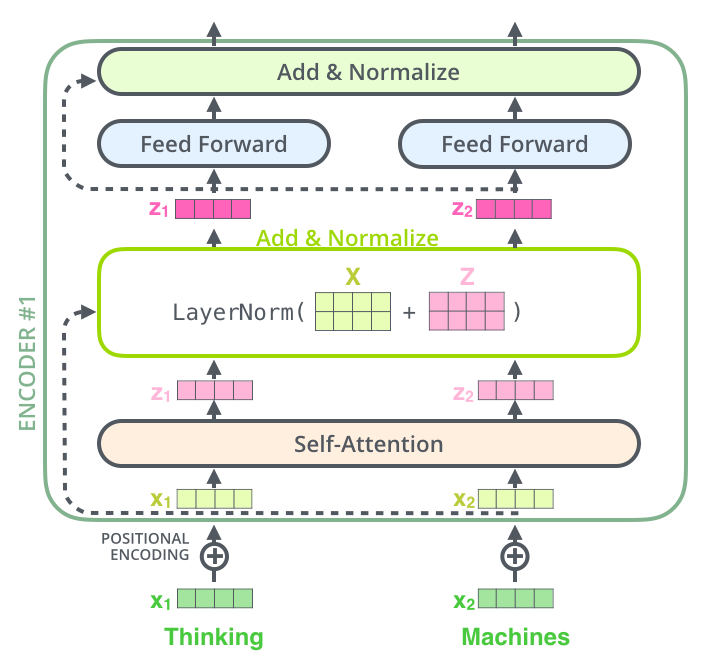
E isso se aplica às subcamadas do Decoder também. Se nós pensarmos em um Transformer de 2 Encoders e Decoders empilhados, seria algo assim:
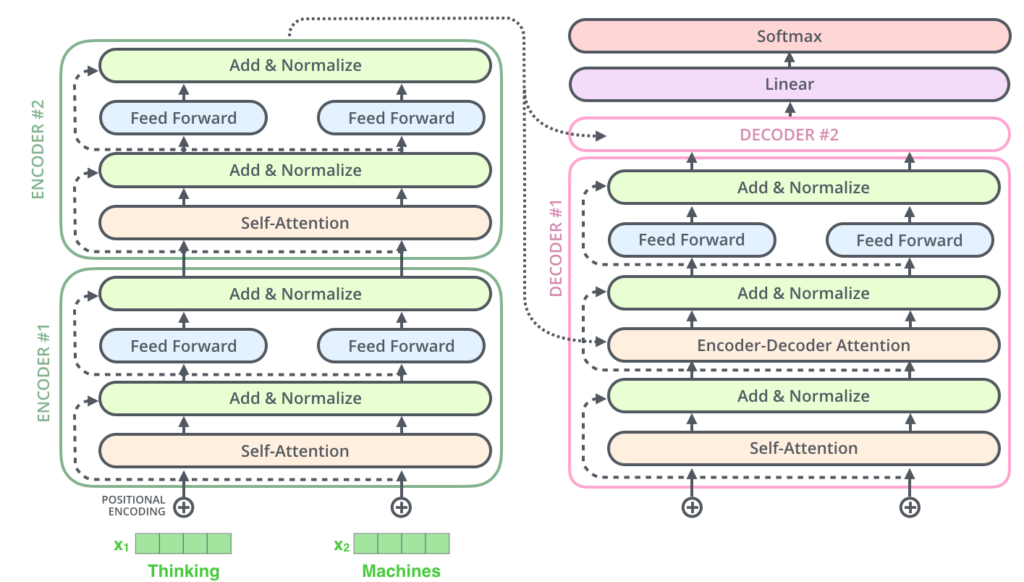
O lado do Decoder
Agora que nós cobrimos a maioria dos conceitos do lado do Encoder, nós basicamente sabemos como os componentes do Decoders funcionam também. Mas agora vamos ver como eles trabalham juntos.
O Encoder começa processando a sequência de entrada. A saída do Encoder superior é então transformada em um conjunto de vetores de Atenção K e V. Estes serão usados por cada Decoder na camada de “Atenção Encoder-Decoder”, que ajuda o Decoder a focar nos lugares apropriados da sequência de entrada.
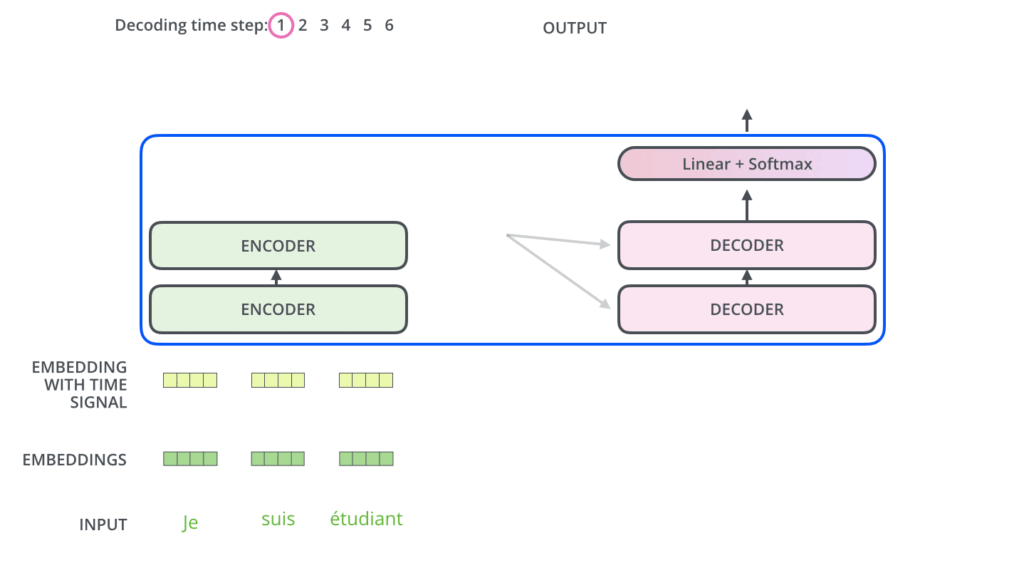
Os próximos passos repetem o processo até que um símbolo especial é alcançado, indicando que o Decoder do Transformer finalizou a sua saída. A saída de cada passo é alimentada no Decoder inferior no passo seguinte, e os Decoders propagam seus resultados de decodificação assim como os Encoders fizeram. E tal como fizemos com as entradas do Encoder, geramos os Embeddings e adicionamos os Encodings Posicionais para as entradas destes Decoders para indicar a posição de cada palavra.
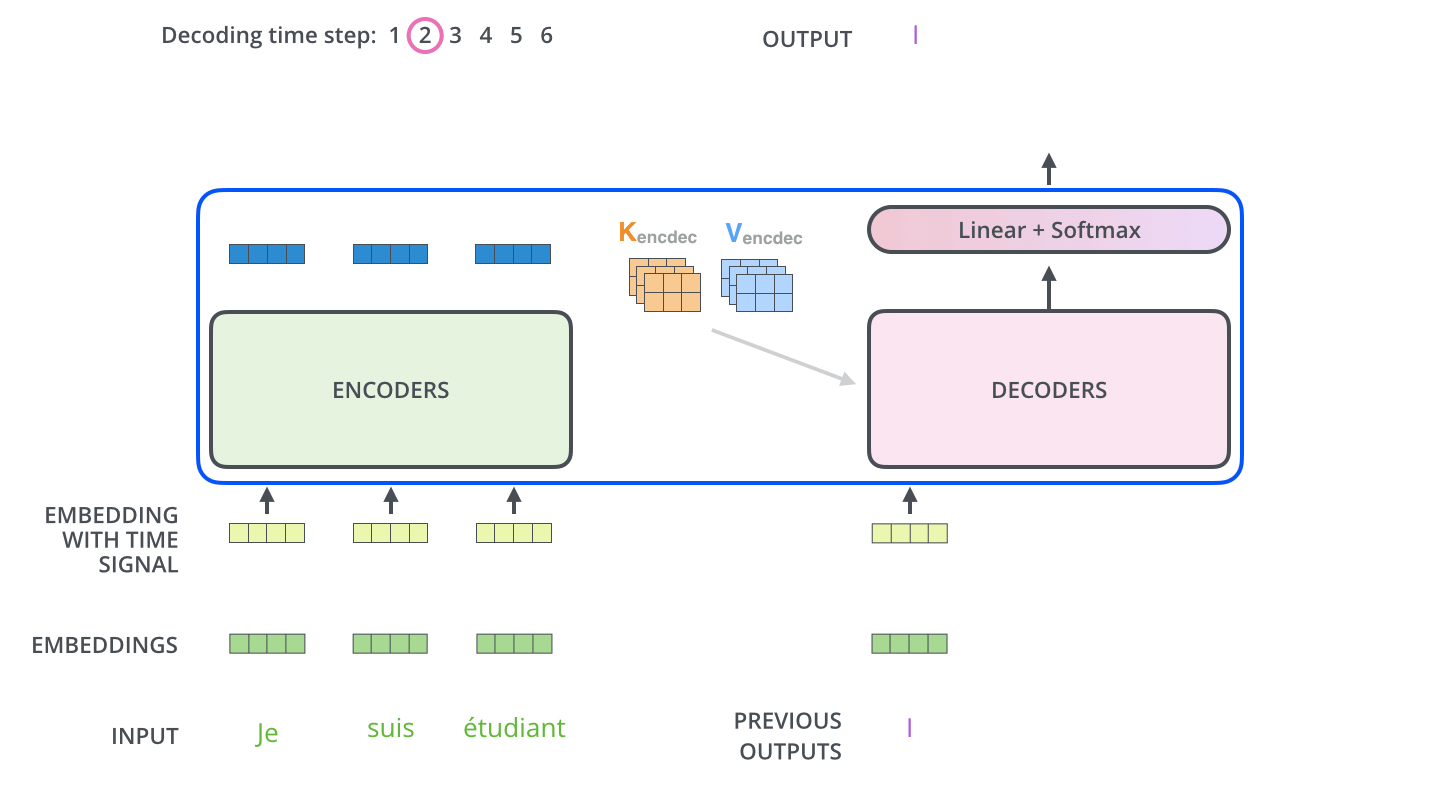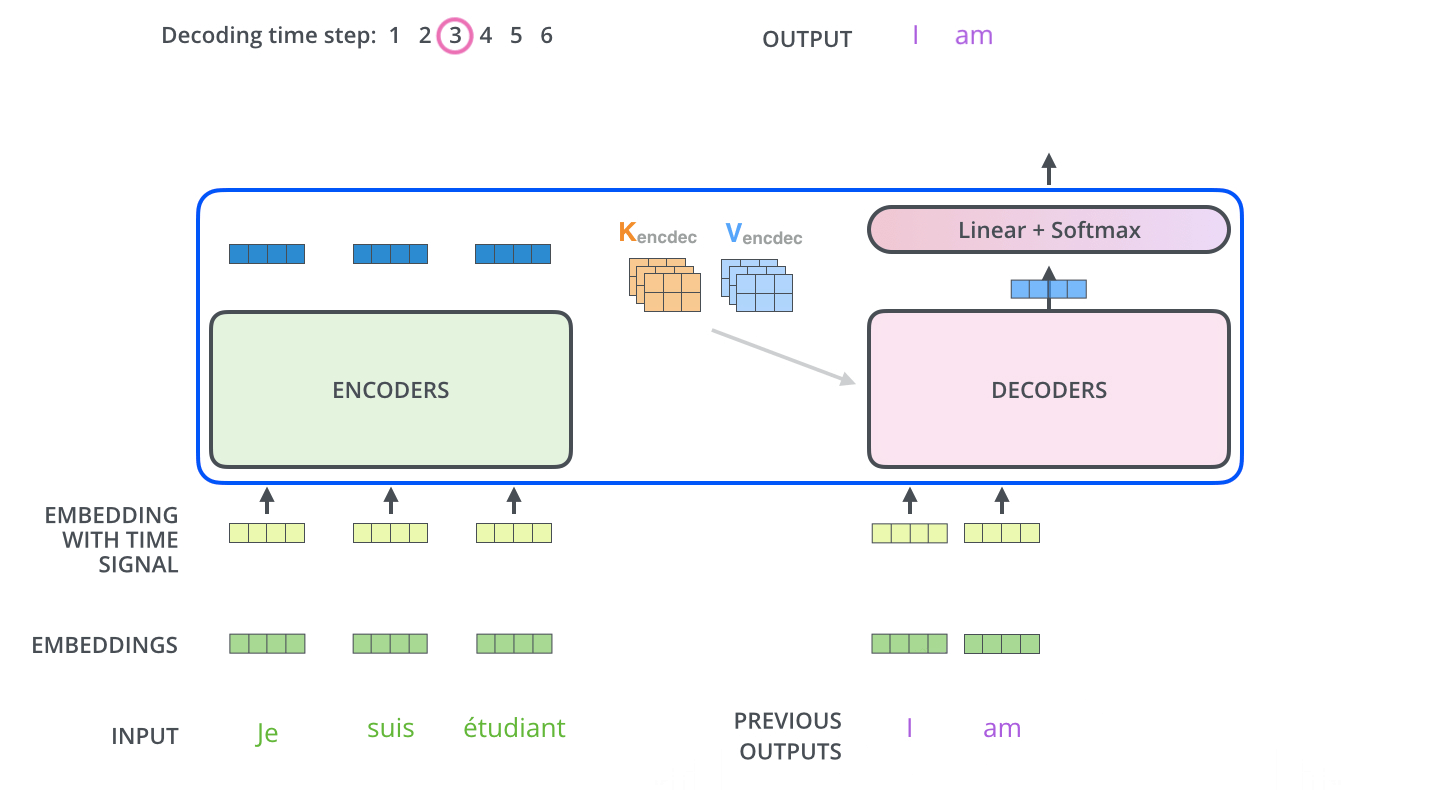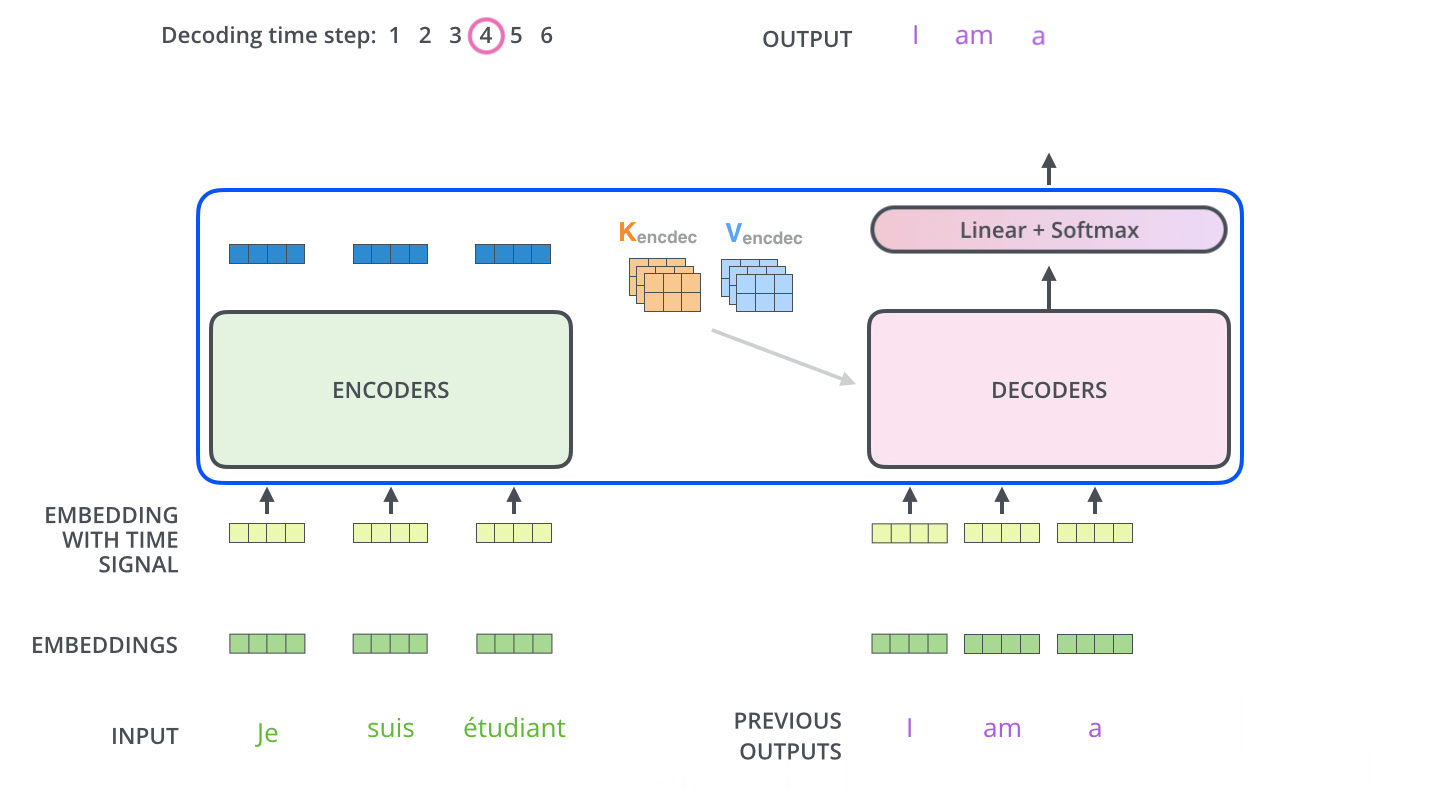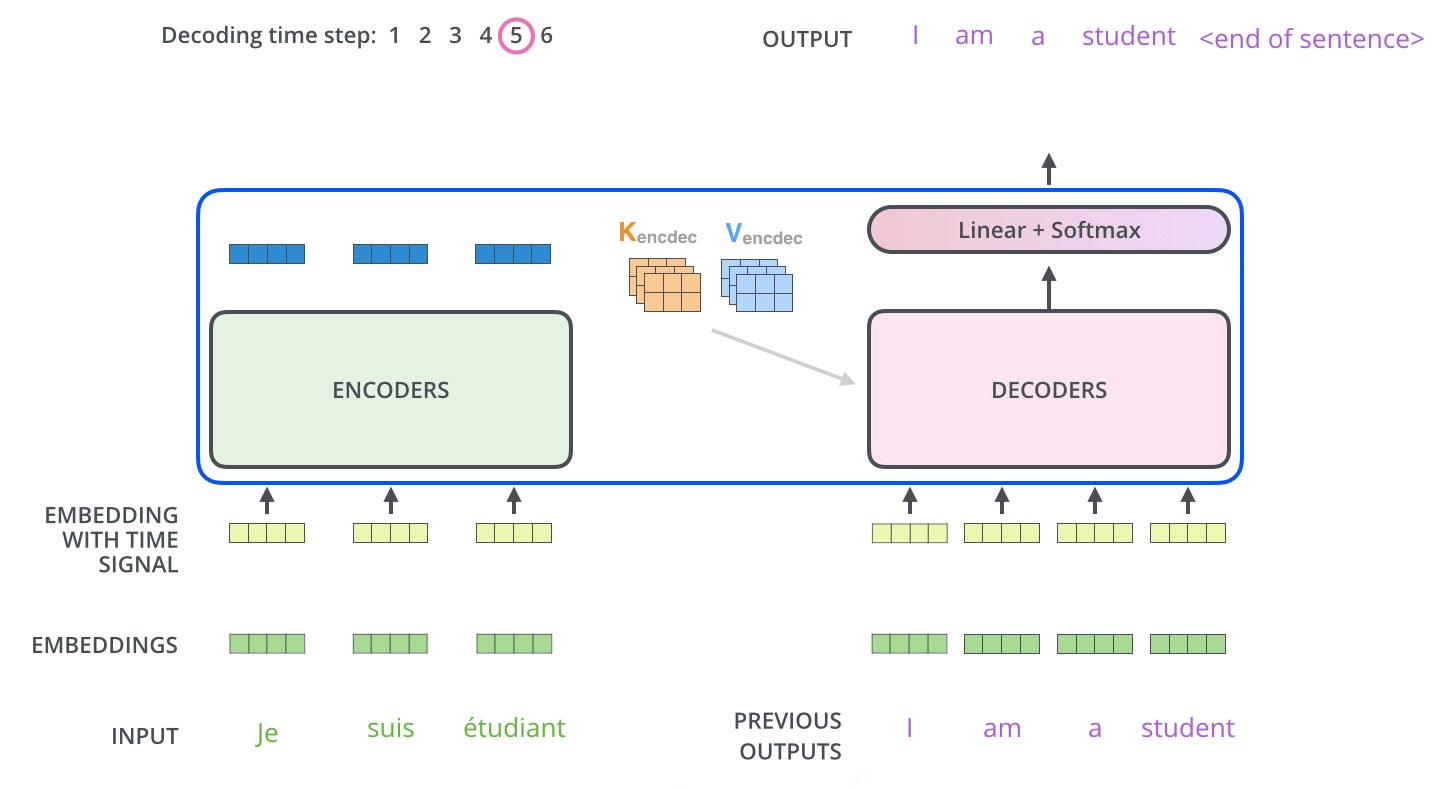
As camadas de Self-Attention no Decoder operam de forma ligeiramente diferente do que as no Encoder.
No Decoder, a camada de Self-Attention só pode se atentar para posições anteriores na sequência de saída. Isso é feito mascarando as posições futuras (as definindo como -inf) antes da etapa de Softmax no cálculo de Self-Attention.
A camada de “Atenção Encoder-Decoder” funciona exatamente como a Multi-Head Self-Attention, exceto que cria a sua matriz de Query da camada de baixo dela, e pega as matrizes Key e Value da saída da pilha de Encoders.
A camada final Linear e de Softmax
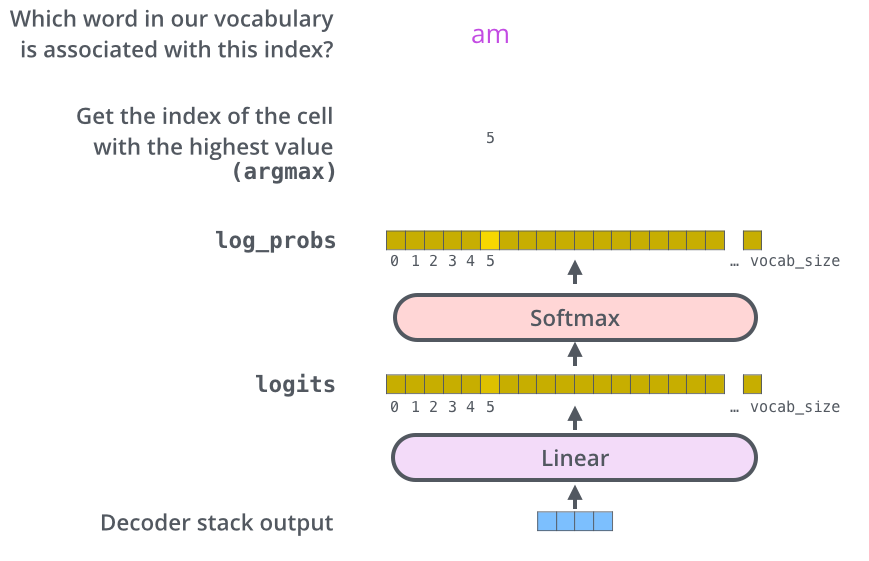
A pilha de Decoders gera um vetor de números decimais (floats). Como transformar isso em uma palavra? Esse é o trabalho da última camada Linear, que é seguida por uma camada de Softmax.
A camada Linear é uma simples rede neural totalmente conectada (Fully Connected) que projeta o vetor produzido pela pilha de Decoders em um vetor muito, muito maior, chamado de vetor de Logits.
Vamos supor que o nosso modelo conhece 10.000 palavras diferentes em Inglês (o “vocabulário de saída” do nosso modelo) que foram aprendidas a partir do conjunto de dados de treinamento. Isso faria que o nosso vetor Logits tivesse uma largura de 10.000 células – cada célula correspondendo ao escore/pontuação de uma única palavra. É assim que interpretamos a saída do modelo após a camada Linear.
A camada Softmax, então, transforma esses escores em escores de probabilidade (todas positivas, somando um total de 1.0). A célula com a probabilidade mais alta é escolhida, e a palavra associada a ela é produzida como saída para esse passo.
Resumo do Treinamento
Agora que cobrimos todo o processo de Forward-Pass, ou “passagem direta”, por um Transformer treinado, seria útil dar uma olhada na ideia por trás do treinamento do modelo.
Durante o treino, um modelo não treinado passaria pelo exato mesmo processo de Forward-Pass. No entanto, como estamos treinando o modelo com um conjunto de dados de treino rotulados, podemos comparar a sua saída com a saída correta real.
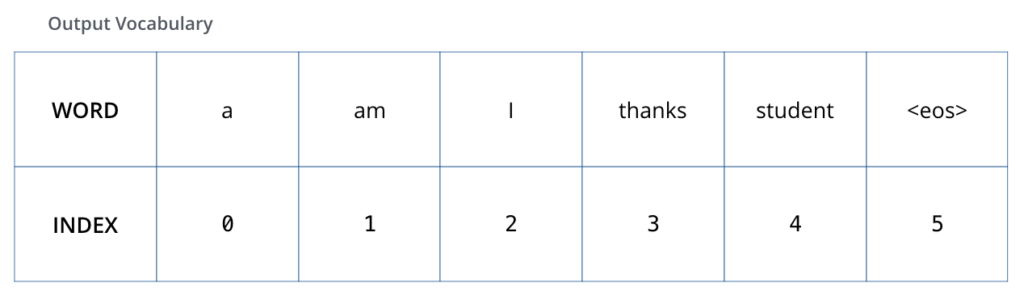
Para visualizar isso, vamos supor que nosso vocabulário de saída contenha apenas seis palavras: “a”, “am”, “i”, “thanks”, “student” e “<eos>” – uma abreviação para <end of sentence>, ou “final da sentença”.
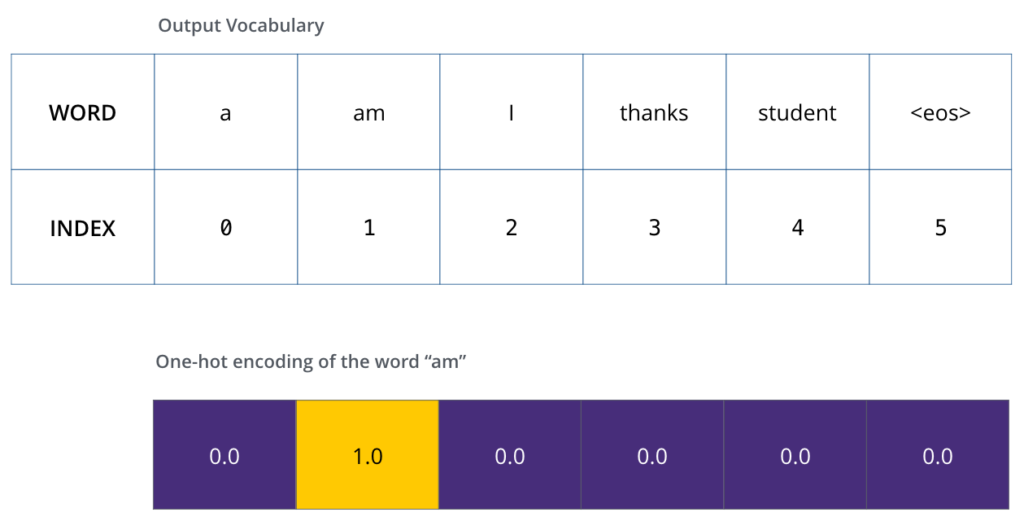
Uma vez que definimos o nosso vocabulário de saída, nós podemos usar um vetor com a mesma largura para indicar cada palavra do nosso vocabulário. Isso também é conhecido como One-Hot Encoding. Então por exemplo, nós podemos indicar a palavra “am” usando o seguinte vetor.
Seguindo neste resumo, vamos discutir a Função de Perda do nosso modelo, também chamada de Loss Function. Esta é a métrica que nós estamos otimizando durante a fase de treino para chegar a um modelo treinado e, esperamos, incrivelmente preciso.
A Função de Perda
Digamos que estamos treinando nosso modelo. Digamos também é que nosso primeiro passo na fase de treinamento, e estamos treinando nosso modelo em um simples exemplo: traduzir “merci” em “thanks”.
O que isso significa é que nós queremos que na saída, a distribuição das probabilidades indique que a palavra “thanks” é a mais provável. Mas dado que o modelo não foi treinado ainda, é improvável que isso aconteça por enquanto.
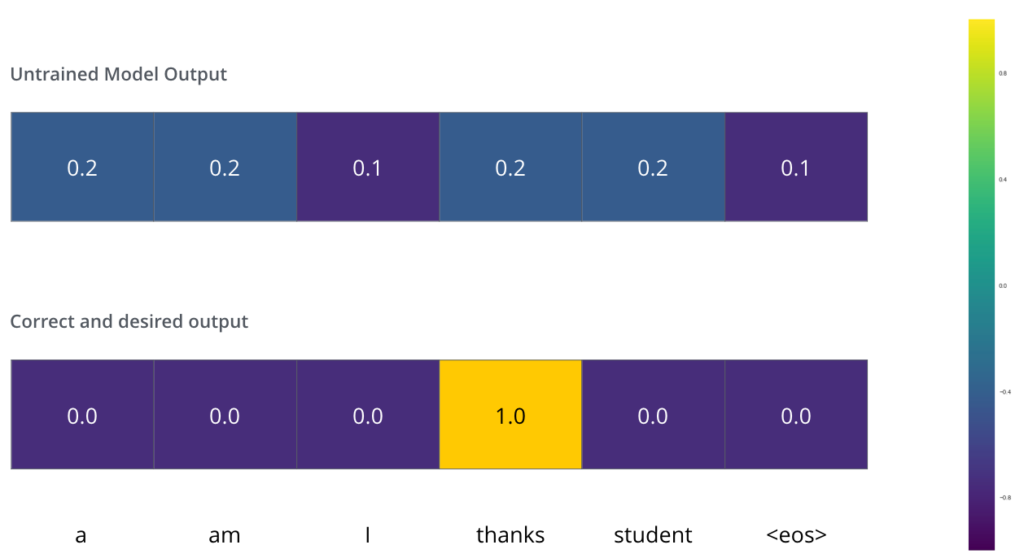
Como nós comparamos duas distribuições de probabilidades? Nós simplesmente subtraímos uma da outra. Para mais detalhes, leia sobre Cross-Entropy e Kullback-Leibler Divergence.
No entanto, note que este é um exemplo simplificado demais. Mais realisticamente, nós vamos ter frases mais longas que uma única palavra. Por exemplo – entrada: “je suis étudiant” e saída esperada: “i am a student”. O que isso de fato significa, é que nós queremos que nosso modelo sucessivamente gere saídas de distribuições de probabilidades onde:
- Cada distribuição de probabilidades é representada por um vetor de tamanho
vocab_size, o tamanho do nosso vocabulário (6 no nosso exemplo simplificado, mas de maneira mais realista, um número como 30.000 ou 50.000). - A primeira distribuição de probabilidades tem a maior probabilidade na célula associada à palavra “i”.
- A segunda distribuição de probabilidades tem a maior probabilidade na célula associada à palavra “am”.
- E assim por diante, até que a quinta distribuição de saída identifique o símbolo
<end of sentence>, que também tem uma célula associada a ele.
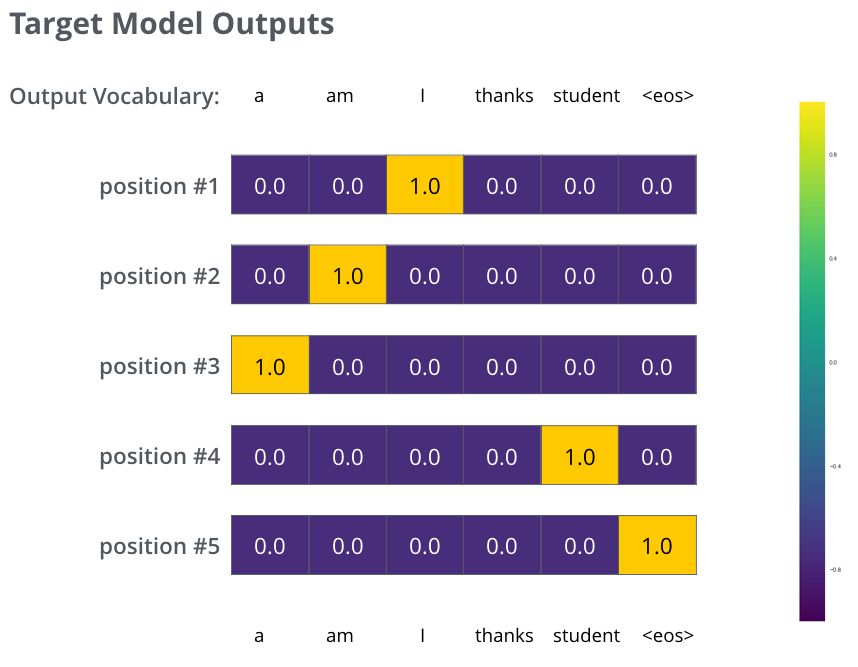
Após treinar o modelo de Transformers por tempo o suficiente em uma base de treino grande o suficiente, nós esperamos que a distribuições de probabilidades estejam como algo assim:
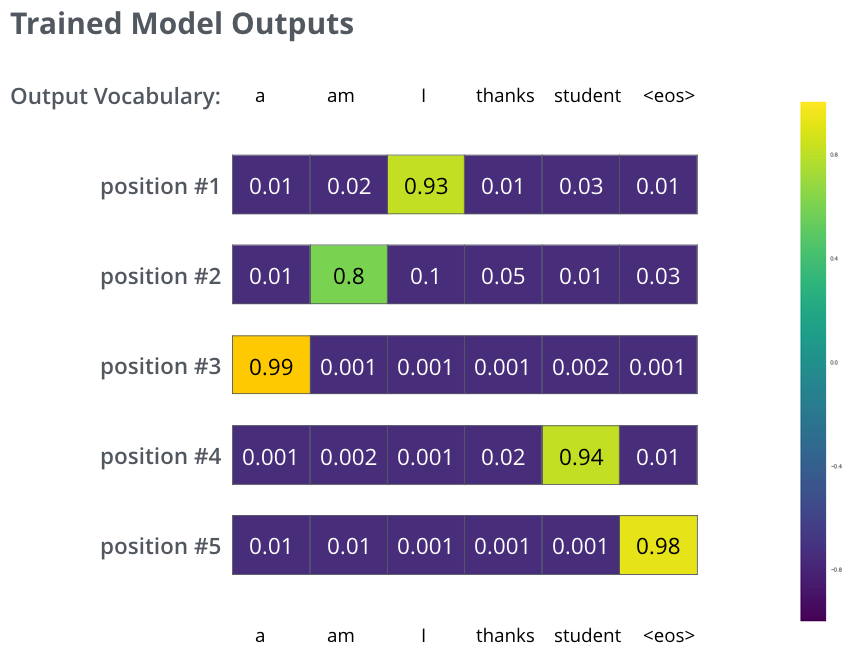
Agora, porque o modelo de Transformers produz as saídas uma de cada vez, podemos supor que o modelo está selecionando a palavra com maior probabilidade dessa distribuição. E descartando as demais. Essa é uma maneira de fazer isso, chamada de Greedy Decoding, ou “decodificação gananciosa”.
Outra maneira de fazer isso seria manter, por exemplo, as duas palavras com maior probabilidade (digamos que “I” e “a” por exemplo). Então, no próximo passo, executar o modelo duas vezes. Uma assumindo que a primeira palavra de saída era “I”. E outra vez assumindo que era a palavra “a”. E a versão que produzir menos erro considerando ambas as posições #1 e #2 é mantida. Repetimos isso para as posições #2 e #3… etc.
Esse método é chamado de Beam Search, ou “busca em feixe”. No nosso exemplo, o beam_size é 2. Isso significa que o tempo todo, duas hipóteses parciais (traduções não concluídas) são mantidas em memória. E as principais opções, os top_beams, também são 2. Significando que retornaremos duas traduções. Ambos são hiperparâmetros com os quais podemos experimentar.
Fonte
Esta foi uma tradução. O conteúdo original está disponível em The Illustrated Transformer. Este e outros ótimos posts podem ser encontrados no blog do Jay Alammar (https://jalammar.github.io/).
Com a autorização do autor original, trouxemos este valioso conteúdo para o BRAINS, em Português. 🇧🇷
Conclusão
A arquitetura de Transformers, e todos os mecanismos que a possibilitam, estão em grande discussão no momento. É muito importante para todos que buscam compreender a forma como encaramos a Inteligência Artificial atualmente, entender estes conceitos. Trouxemos um dos posts mais famosos do mundo sobre o tema para ajudar nossos colegas brasileiros que não falam Inglês.
Se você quiser também colaborar trazendo conteúdo sobre ML, IA e Dados para o Brasil, em Português, conheça nossa comunidade. E para entender melhor nosso propósito e saber como colaborar, leia nosso post de introdução do BRAINS – Brazilian AI Networks.
Caso tenha ficado com alguma dúvida, entre em contato com a gente. Se conhecer outros conteúdos bons como este, nos indique para tradução. Estamos pouco a pouco mergulhando mais fundo no mundo dos Foundation Models, dos Transformers e da IA Generativa.
Contamos com vocês para crescer nossa comunidade. Até porque…




1 comentário