Imagine que você está ajudando uma amiga a avaliar se uma casa com 185 m² e um valor de US$ 400.000 é um bom negócio. Com base em referências e cálculos simples, começamos a construir a base de uma rede neural, introduzindo os fundamentos necessários para entender como esses modelos podem ser treinados para fazer previsões.
Este guia é uma tradução do artigo original de Jay Alammar, renomado por sua abordagem clara e acessível no ensino de redes neurais.
Começa aqui
Vamos começar com um pequeno exemplo, digamos que você está ajudando uma amiga que quer comprar uma casa. Foi cotada em US$400.000 uma casa de 185 m² (2000 sq ft ). Este é um bom preço, ou não?
Não é fácil dizer sem uma referência. Então você pergunta para seus amigos que compraram casas nos mesmos bairros e consegue três dados:
Particularmente, minha primeira ideia seria obter o preço do metro quadrado (sq ft). Isso equivale a US$180 por metro quadrado.
Com isso seja bem-vindo a sua primeira rede neural! Ainda não estamos no nível da Siri, mas agora você conhece o alicerce principal. Ela é representada assim:
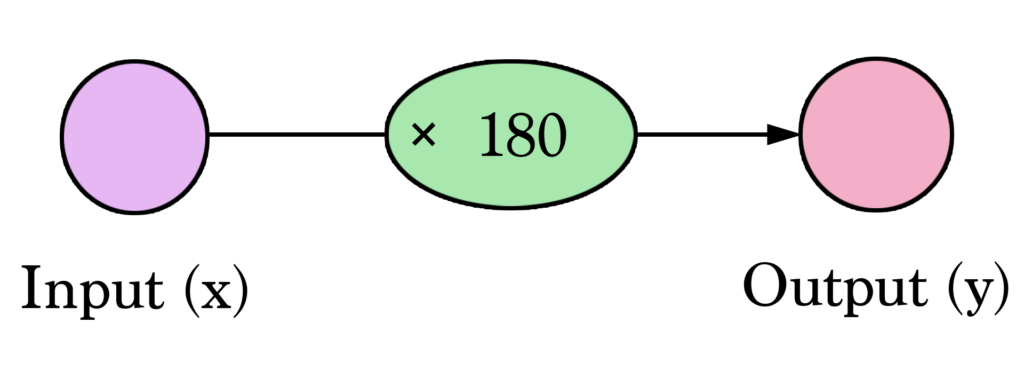
Diagramas como esse mostram a estrutura da rede e como calcular uma predição. O cálculo começa a partir do Input (Entrada) na esquerda. O valor do input passa para a direita, ele é multiplicado pelo Peso e o resultado se torna nosso Output (Saída).
Multiplicando 2000 sq ft por 180 temos US$360.000. Isso é tudo que tem nessa camada. Calcular a predição é uma simples multiplicação. Mas antes disso, nós precisamos pensar no peso pelo qual multiplicaremos. Aqui começamos com uma média, depois veremos algoritmos melhores que podem ser escalonados à medida que obtemos mais inputs e modelos mais complexos. Encontrar o peso é a nossa etapa de “treinamento”. Portanto, sempre que você ouvir alguém “treinando” uma rede natural, isso significa apenas encontrar os pesos que usamos para calcular uma predição.
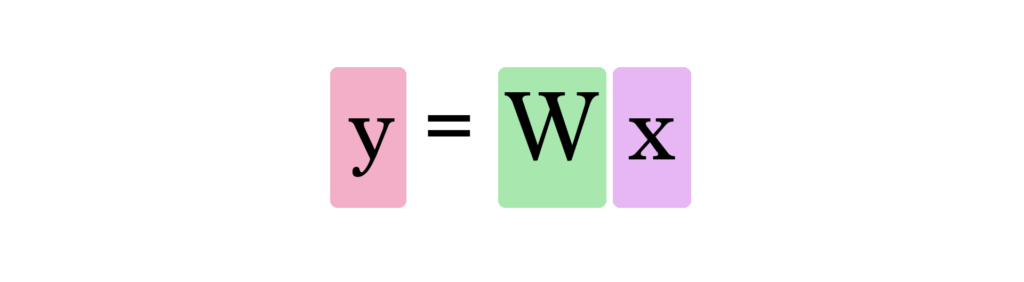
Isso é um modelo de predição simples que pega um input, faz um cálculo, e nos dá um output (uma vez que o output pode ser de valores contínuos, o nome técnico para o que temos seria um “modelo de regressão”).
Vamos visualizar esse processo (para simplificar, vamos mudar nossa unidade de preço de $1 para $1.000. Agora nosso peso é 0.180 em vez de 180):
Mais Difícil, Melhor, Mais Rápido, Mais Forte
Podemos ir além do que estimar o preço com base na média dos nossos dados?
Vamos tentar!
Primeiro definiremos o que significa ir além nesse cenário. Se nós aplicarmos nosso modelo aos três pontos de dados que temos, quão bom ele seria?
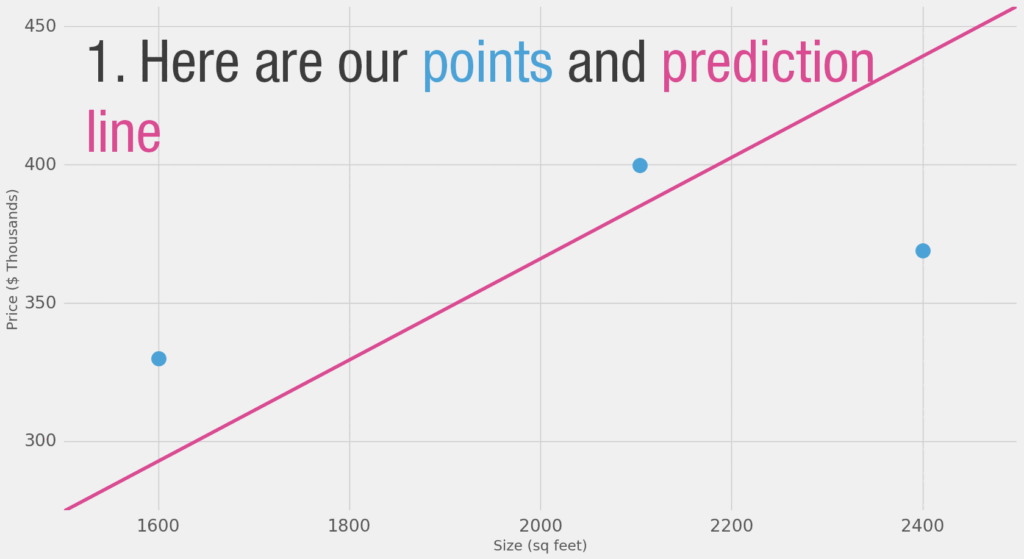
Temos um pouco de amarelo. Amarelo é ruim, amarelo significa erro. Queremos diminuir o amarelo o máximo que puder.
Aqui podemos ver o valor do preço atual, o valor da predição do preço, e a diferença entre eles. Em seguida, precisaremos calcular a média dessas diferenças, assim teremos um número que nos dirá a quantidade de erro que existe nesse modelo de predição. O problema é que na terceira linha temos o valor -63. Teremos que lidar com esse valor negativo se quisermos usar a diferença entre a predição e o preço como nossa medida de erro. Essa é a razão pela qual eu adicionei uma nova coluna que mostra o erro ao quadrado, eliminando assim o valor negativo.
Para entender um pouco mais sobre o processo de Regressão Linear e as diferentes formas de calcular os seus erros, recomendo o post Modelos de Regressão: Regressão Linear, aqui no BRAINS.
Essa é nossa definição de ir além, um modelo melhor é aquele que tem menos erros. O erro é medido com a média dos erros para cada ponto do nosso conjunto de dados. Para cada ponto, o erro é medido pela diferença entre o valor real e o valor predito, elevado à segunda potência. Isso é chamado Erro Quadrático Médio. Usá-lo como um guia para treinar nosso modelo, torna-o nossa função de perda (e também, função de custo), chamados na literatura de Loss Function ou Cost Function.
Agora que encontramos nossa medida para definir o que constitui um modelo melhor, vamos experimentar mais alguns valores de peso e compará-los com nossa escolha média:
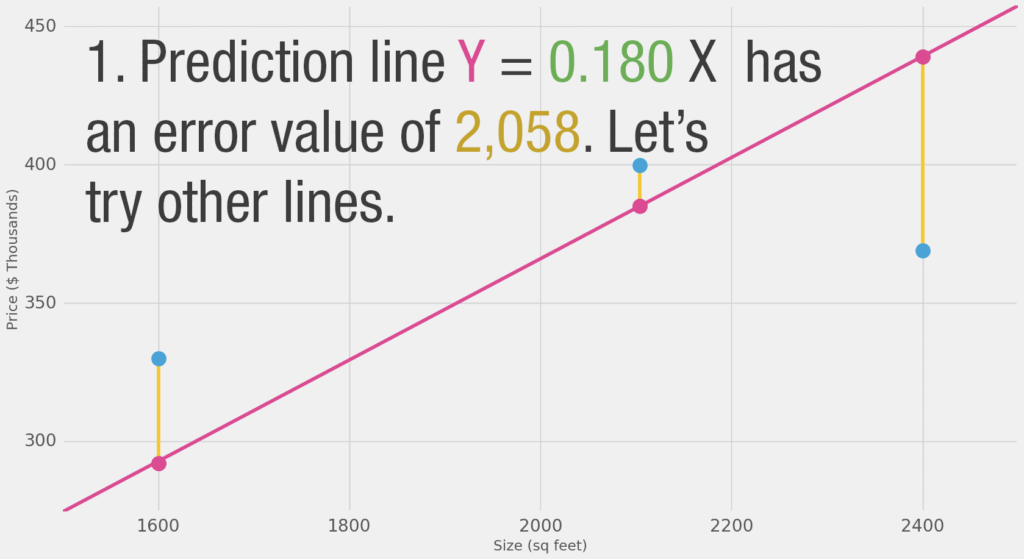
Nossas retas, podem se aproximar mais de nossos valores agora que temos esse valor b adicionado à fórmula da reta. Nesse contexto, chamamos isso de “viés”. Isso faz com que nossa rede neural fique assim:
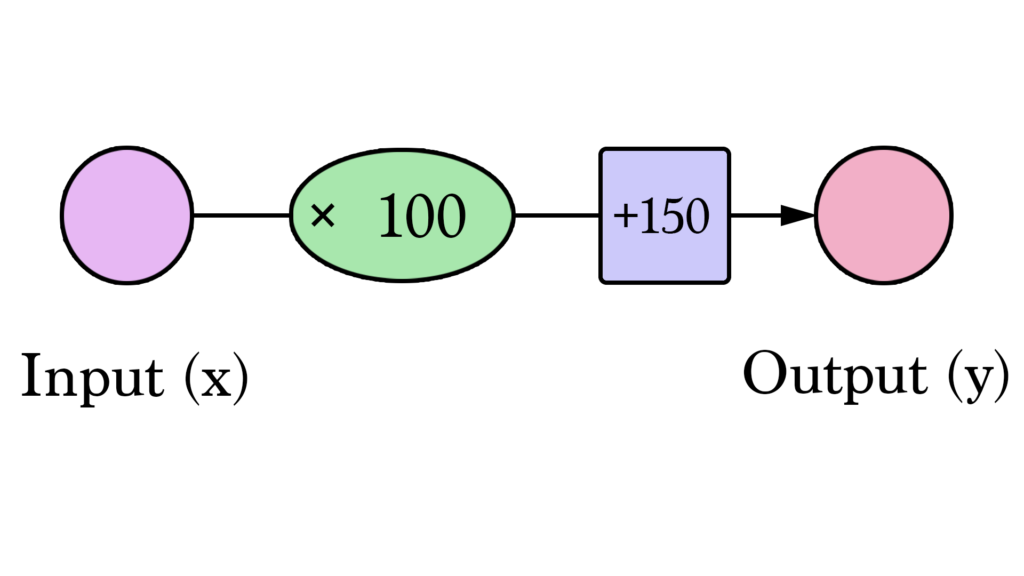
Podemos generalizar dizendo que uma rede neural com um input e um output (aviso de spoilers: e sem camadas ocultas) se parece com isto:
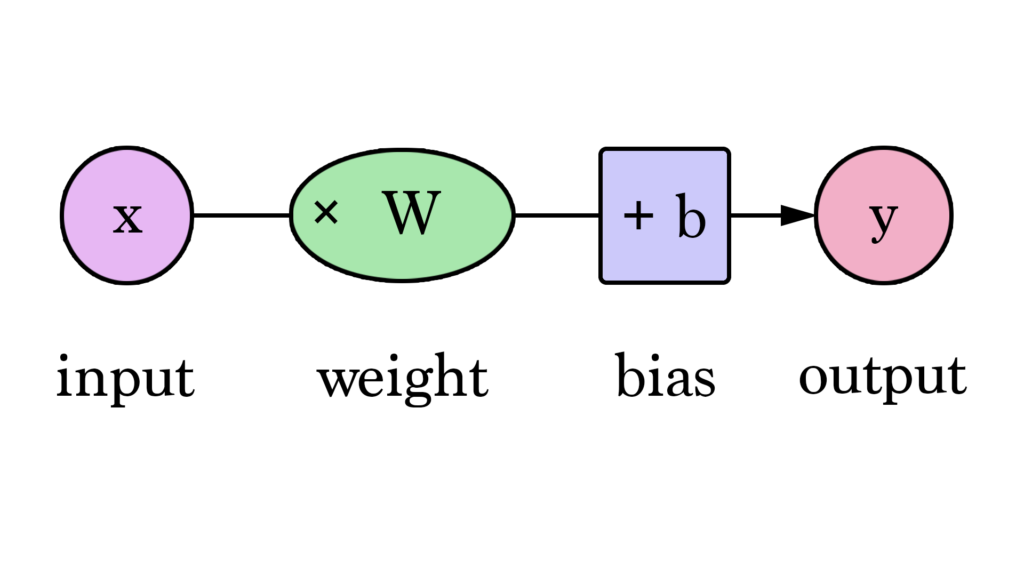
Neste gráfico, W e b são valores que encontramos durante o processo de treinamento. X é o input que inserimos na fórmula (área em sq ft no nosso exemplo). Y é o preço predito.
Agora usamos essa fórmula para calcular uma predição:
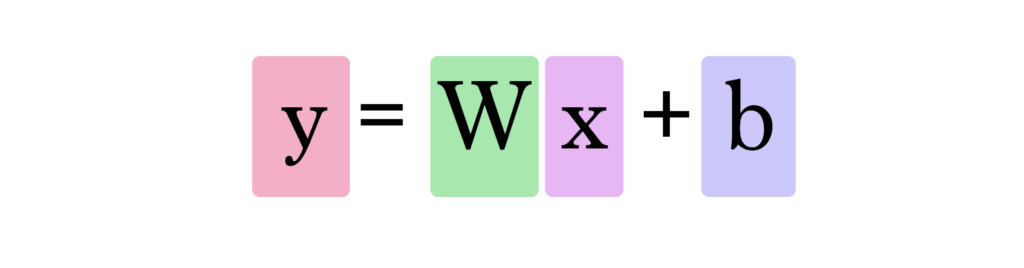
Portanto, nosso modelo atual calcula as predições inserindo a área da casa como x nessa fórmula:
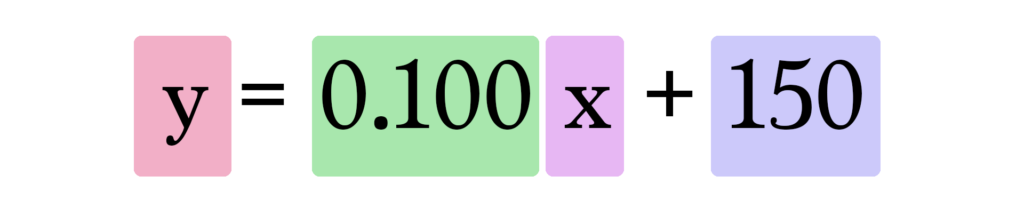
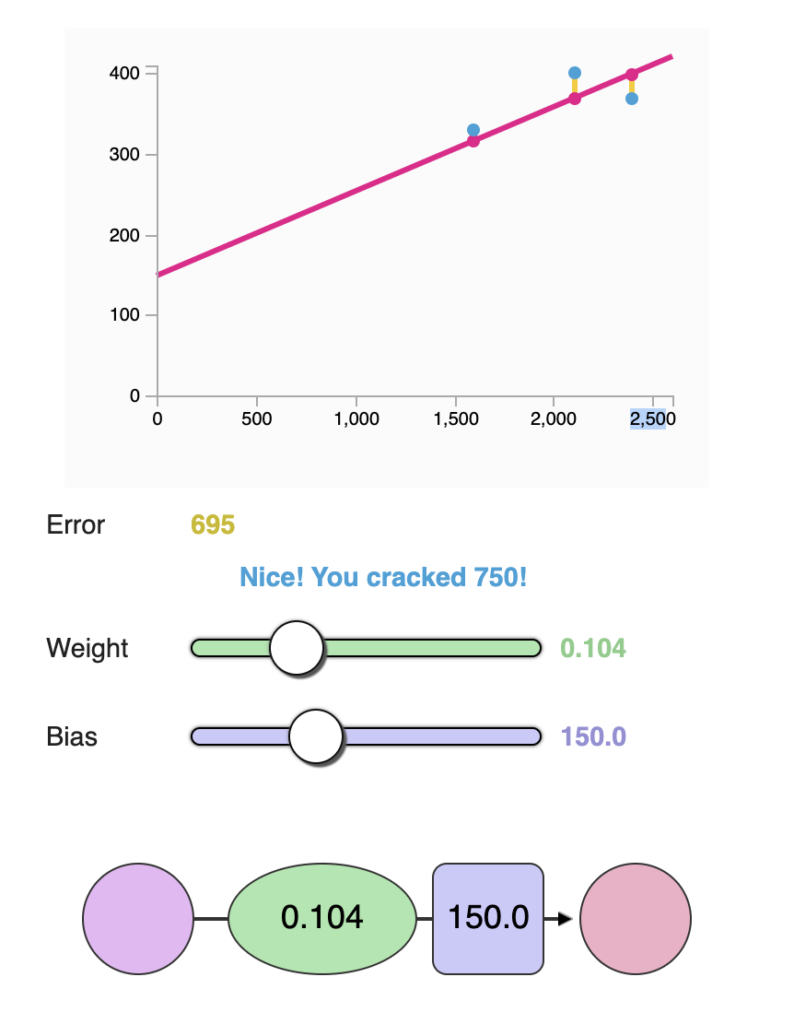
Treine seu Dragão
Que tal brincar de treinar nossa rede neural? Minimize a função de perda ajustando o peso e a polarização. Você consegue obter um valor de erro abaixo de 799?
(Para testar acesse o link do artigo original: https://jalammar.github.io/visual-interactive-guide-basics-neural-networks/#train_your_dragon)
Automação
Parabéns por treinar manualmente sua primeira rede neural! Vamos ver como automatizar esse processo de treino. Abaixo temos outro exemplo com uma funcionalidade adicional semelhante a um piloto automático. Esses são os botões GD Step. Eles usam um algoritmo chamado “Método do Gradiente” para tentar avançar em direção ao valores corretos de peso e polarização que minimizam a função de perda.
(Para testar acesse o link do artigo original: https://jalammar.github.io/visual-interactive-guide-basics-neural-networks/#automation)
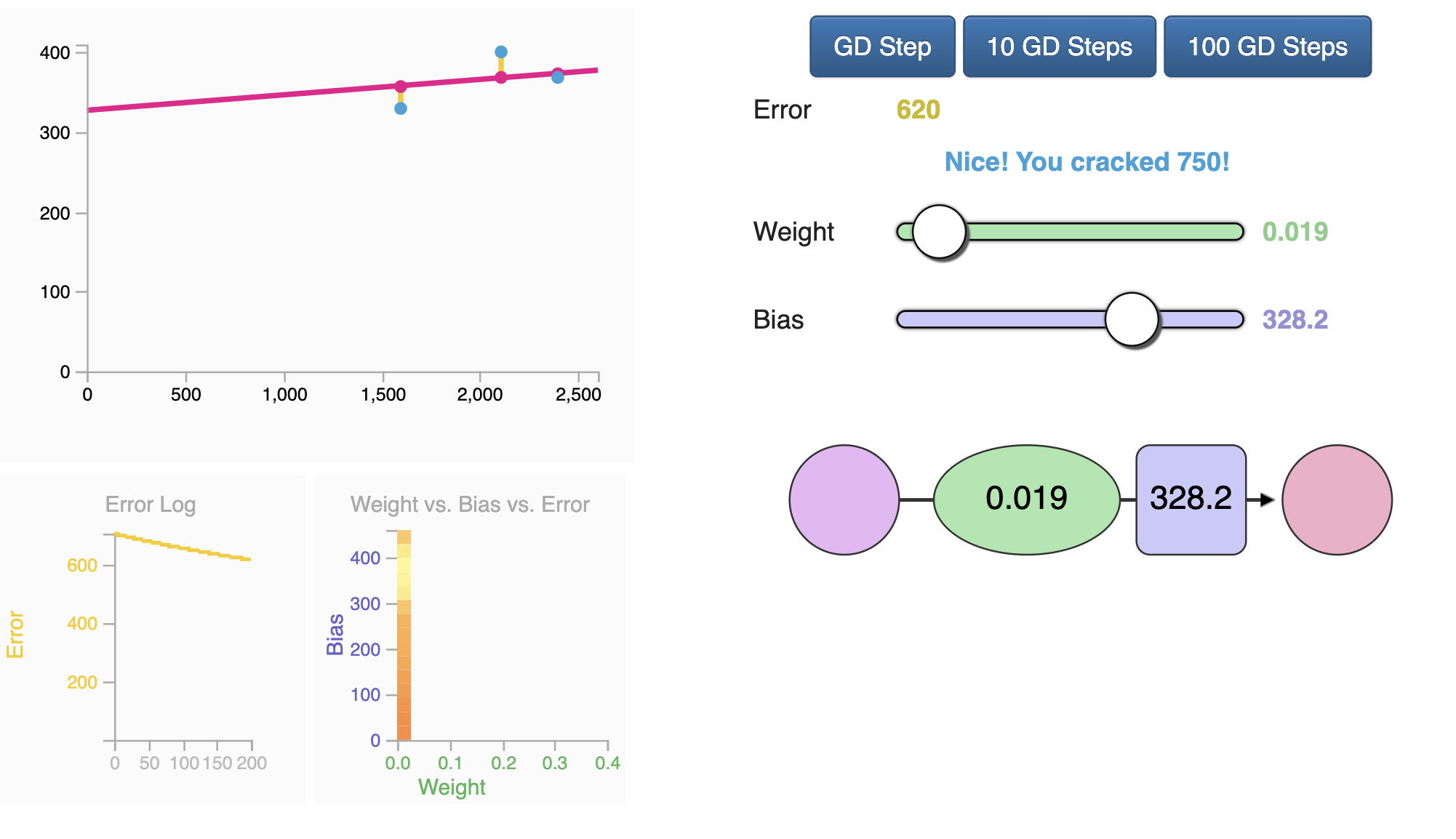
Os dois novos gráficos servem para ajuda-lo a rastrear os valores de erro enquanto você mexe nos parâmetros (peso e viés) do modelo. É importante acompanhar o erro, pois o processo de treinamento visa reduzi-lo o máximo possível.
Como o método gradiente sabe onde deve ser o próximo passo? Cálculo! Veja, conhecendo a função que estamos minimizando (nossa função de perda, a média de (y_ – y)² para todos os nosso pontos de dados), e conhecendo os inputs atuais (o peso e o viés atuais), as derivadas da função de perda nos dizem em que direção deslocar W e b para minimizar o erro.
Aprenda mais sobre método gradiente e como usa-lo para calcular os novos pesos e viés nas primeiras aulas do curso de Machine Learning do Coursera.
E Então Haviam Dois
O tamanho da casa é a única variável que influencia no preço? Obviamente existem muitos outros fatores. Vamos adicionar outra variável e ver como podemos ajustar nossa rede neural a ela.
Digamos que sua amiga pesquise um pouco mais e encontre mais data points. Ela também descobre quantos banheiros cada casa tem:
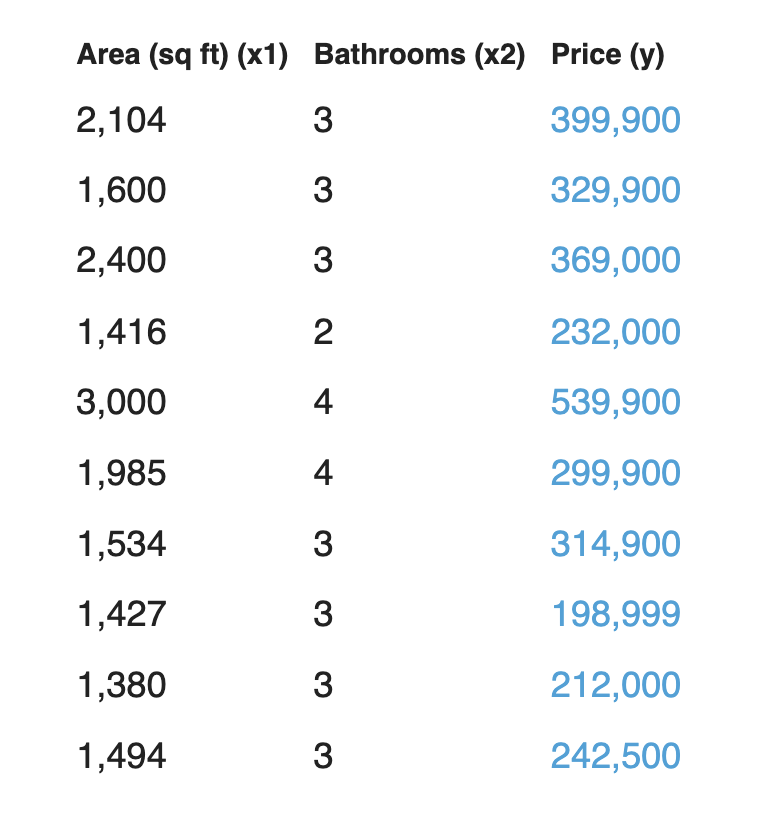
Nossa rede neural com duas variáveis se parece assim:
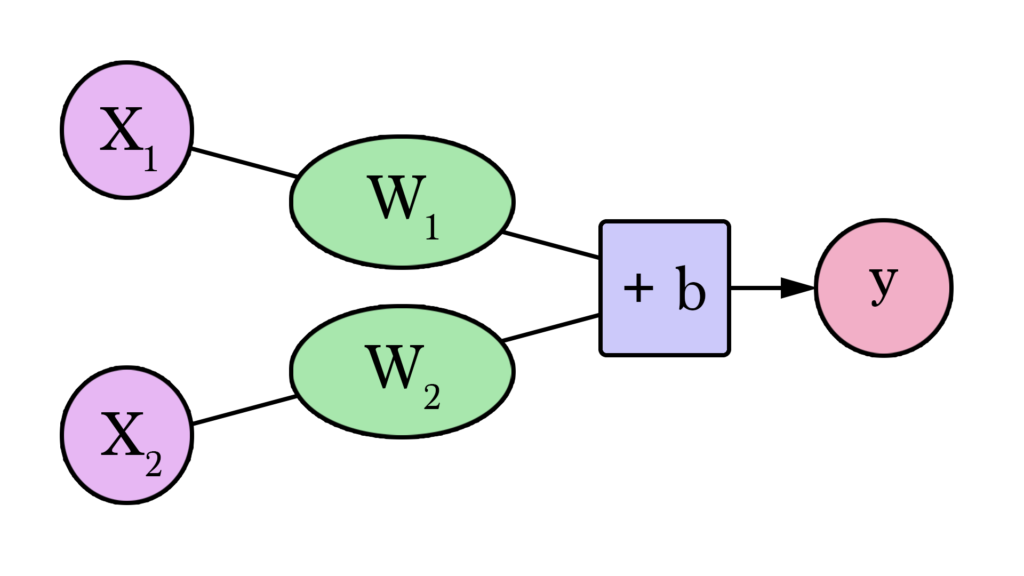
Agora temos dois pesos (um para cada input) e um viés para criar nosso novo modelo.
O cálculo de Y fica assim:

Mas como encontraremos w1 e w2? Isso é um pouco mais complicado do que quando precisávamos nos preocupar apenas com um valor de peso. Quanto é que ter um banheiro extra altera a forma como prevemos o valor da casa?
Tente encontrar os pesos e os vieses corretos. Você começara a ver a complexidade qua acabamos entrando à medida que o número de nossos inputs aumenta. Começamos a perder a capacidade de criar formas 2D simples que nos permitem vizualizar o modelo rapidamente. Em vez disso teremos que confiar principalmente em como o valor do erro está evoluindo a medida que ajustamos os parâmetros do nosso modelo.
(Para testar acesse o link do artigo original: https://jalammar.github.io/visual-interactive-guide-basics-neural-networks/#two)
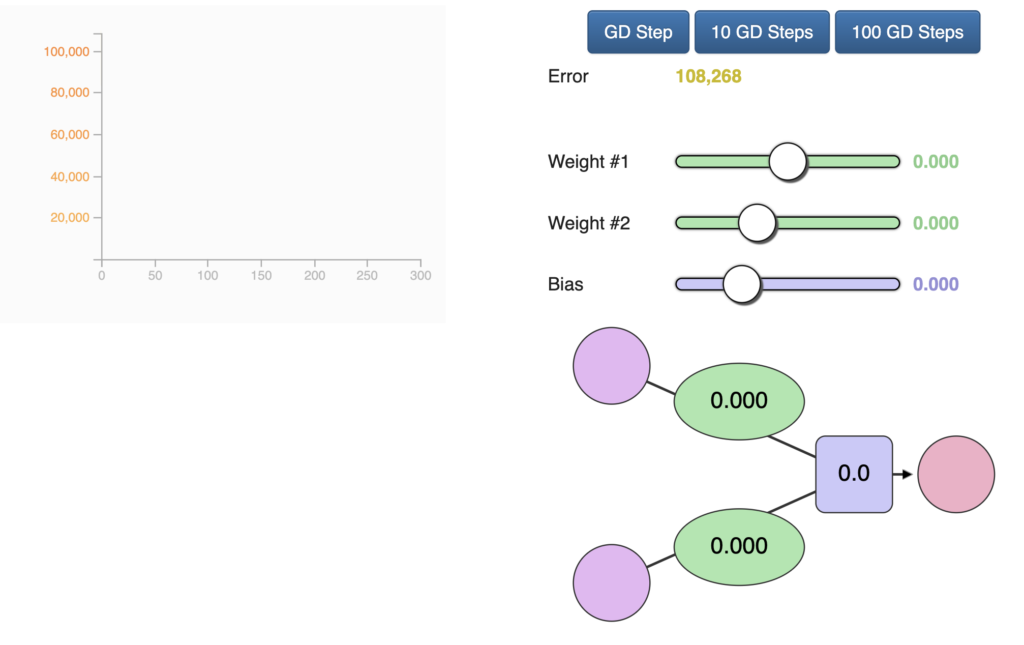
Nosso confiável método gradiente está aqui para ajudar mais uma vez. Ainda é valioso para nos ajudar a encontrar os pesos e os vieses corretos.
Features
Agora que você viu redes neurais com uma e duas variáveis, você pode descobrir como adicionar variáveis e usa-las para calcular suas predições. O número de pesos continuará a crescer e nossa implementação do método gradiente terá que ser ajustada a medida que adicionamos cada variável, para que possa atualizar os novos pesos associados a nova variável.
É importante notar que não alimentamos a rede com todas as informações que temos sobre nossos exemplos. Temos que ser seletivos com qual variável vamos alimentar o modelo. A seleção/processamento de variáveis é uma disciplina inteira com seus próprios conjuntos de boas práticas e considerações.
Se você quer ver um exemplo do processo de examinar um dataset para escolher qual variável alimentar o modelo, confira A Journey Through Titanic. É um notebook onde Omar EL Gabry narra seu processo resolvendo o desafio do Titanic no Kaggle. O Kaggle disponibiliza o manifesto do passageiro do Titanic incluindo dados como nome, sexo, idade, cabine e se a pessoa sobreviveu ou não. O desafio é construir um modelo que prediz se uma pessoa sobreviveu ou não, dadas as outras informações.
Classificação
Vamos continuar ajustando nosso exemplo. Assuma que sua amiga lhe deu uma lista de casas. Desta vez, ela marcou quais ela acha que tem um bom tamanho e uma boa quantidade de banheiros:

Ela precisa que você use isso para criar um modelo que predita se ela vai gostar da casa ou não, dado seu tamanho e seu número de banheiros. Você vai usar essa lista acima para construir o modelo, então ela usará o modelo para classificar varias outras casas. Uma mudança adicional no processo, é que ela tem uma outra lista de 10 casas rotuladas, mas ela está escondendo isso de você. Essa outra lista seria usada para validar o modelo depois que você treiná-lo – tentando assim garantir que o modelo compreenda as condições que fazem ela gostar das características da casa.
As redes neurais que brincamos até agora estão todas fazendo “regressão” – elas calculam e geram um valor “contínuo” ( o output pode ser 4, ou 100,6, ou 2143,342343). Na prática, embora, redes neurais sejam geralmente mais usadas em problemas do tipo “classificação”. Nestes problemas, o output das redes neurais deve ser proveniente de um conjunto de valores discretos (ou “classes”) como “Bom” ou “Ruim”. Na prática, teremos um modelo que dirá que há 75% de de certeza de que uma casa é “Boa” em vez de apenas chutar se é “boa” ou “ruim”.

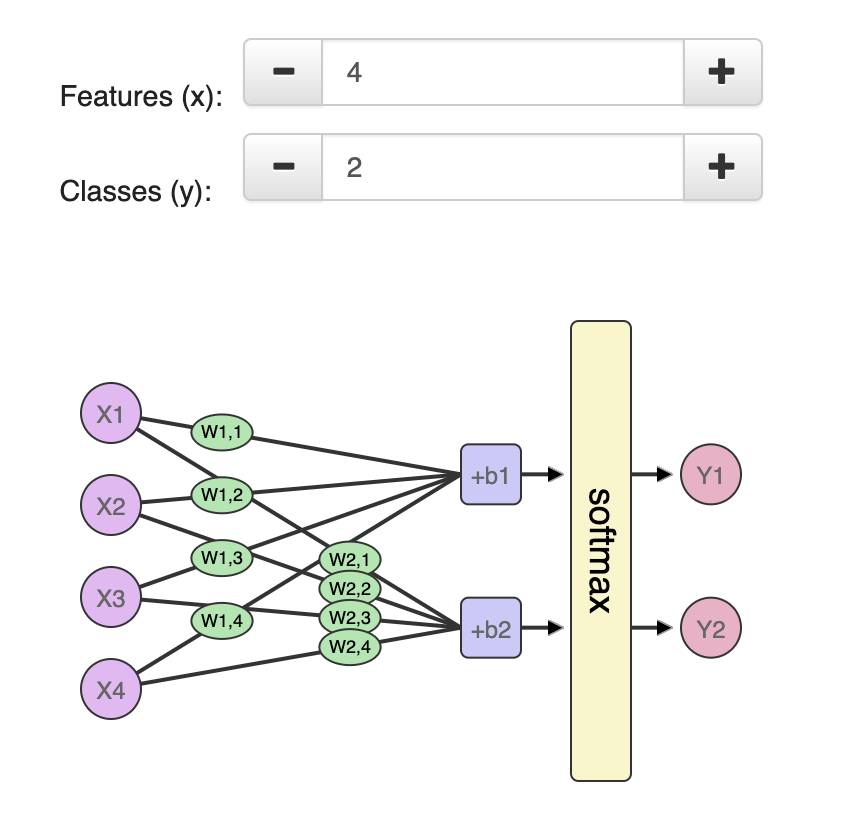
Uma maneira de transformar a rede que vimos em uma rede de classificação, é fazer com que ela produza dois valores – um para cada classe (nossas classes agora serão “bom” ou “ruim”). Nos passamos esses valores através de uma operação chamada “softmax“. O output do softmax é a probabilidade de cada classe. Por exemplo, digamos que aquela camada da rede produz 2 para “bom” e 4 para “ruim” e alimentarmos [2,4] no softmax, ele retornará [0,11, 0,88] como output. O que traduz os valores para dizer que a rede tem 88% de certeza de que o valor inserido é “ruim” e que nossa amiga não gostaria daquela casa.
O softmax pega um array e gera um array do mesmo comprimento. Observe que seus outputs são todos positivos e somam 1 – o que é útil quando geramos um valor de probabilidade. Observe também que mesmo que 4 seja o dobro de 2, sua probabilidade não é apenas o dobro, mas é oito vezes maior que 2. Esta é uma propriedade útil que aumenta a diferença no output, melhorando assim o nosso processo de treinamento.

Fonte
Esta foi uma tradução. O conteúdo original está disponível no artigo A Visual and Interactive Guide to the Basics of Neural Networks. Este é um dos excelentes posts que podem ser encontrados no blog do Jay Alammar (https://jalammar.github.io/).
Com a autorização do autor original, trouxemos este valioso conteúdo para o BRAINS, em Português.
Conclusão
Ao longo deste guia, passamos da simples multiplicação de entradas por pesos até a construção de redes neurais mais complexas que incorporam múltiplas variáveis e utilizam algoritmos de otimização avançados. Com isso, mostramos como ajustar e treinar uma rede neural para minimizar erros e melhorar a precisão das previsões. Esperamos que esta introdução forneça uma base sólida para que você possa avançar em seu aprendizado sobre redes neurais e explorar suas aplicações práticas em diversos campos.
Se você também deseja contribuir trazendo conteúdo sobre ML, IA e Dados para o Brasil, em português, conheça nossa comunidade. Para entender melhor nosso propósito e saber como colaborar, leia nosso post de introdução do BRAINS – Brazilian AI Networks.
Caso tenha alguma dúvida, entre em contato conosco. Se conhecer outros conteúdos bons como este, nos indique para tradução.