Nós começamos a conversar sobre Machine Learning aqui no BRAINS no nosso post Primeiramente, o que é Machine Learning? Se você não leu o post e não está familiarizado com termos como Aprendizado Supervisionado, Base de Treino, Variável Alvo, Regressão, Classificação… Bom, recomendo que leia o post antes. Se você conhece os termos e não leu o post, ainda assim pode servir como uma boa revisão. Aqui iremos abordar exclusivamente o modelo de Regressão Linear.
Falamos um pouco sobre Regressão quando explicamos o que é o Aprendizado Supervisionado, mostrando com exemplos que são técnicas usadas quando buscamos prever, ou predizer, valores contínuos. Ou seja, qualquer valor que vá de menos infinito a mais infinito – ou qualquer valor que faça sentido dentro da realidade do modelo.
Alguns exemplos do uso de técnicas de Regressão são tentar prever o valor de determinado produto ou bem, como por exemplo o valor de um imóvel. Podemos tentar prever a receita de uma empresa, as vendas de um produto ou serviço, o valor de uma ação no mercado financeiro, ou até mesmo para aplicações mais especializadas, como em pesquisas médicas que tentam entender a relação entre a dosagem de uma medicação e a pressão arterial dos pacientes.
O Aprendizado Supervisionado das Regressões
Como já conversamos, algoritmos de Machine Learning tentam encontrar padrões nos dados. Padrões esses que façam sentido nos dados históricos e que possam ser aplicados nos dados futuros. Essa é a essência de qualquer algoritmo.
No caso das Regressões, para podermos tentar prever esse tal valor de interesse (o valor, as vendas, a pressão arterial, etc) nós precisamos fornecer ao nosso modelo exemplos. Mas o que são esses exemplos?
Se vocês se lembram bem, nossos modelos irão mapear uma entrada (input) \(X\) à uma saída (output) \(y\).
\[ X \longrightarrow y \]
Vamos ser mais específicos. O que seria exatamente a entrada (input) \(X\) e a saída (output) \(y\)? Para sermos bem didáticos, vamos trabalhar sobre o exemplo da predição do preço de imóveis.
Primeiro, vamos definir a saída \(y\), que vai ser nossa variável alvo (target). Essa é a variável que nós queremos prever no futuro, neste caso, o valor do imóvel.
A entrada \(X\) vão ser todas as variáveis que influenciam a saída \(y\), ou seja, as características (features) do imóvel. Então podemos ter como entrada \(X\), por exemplo, a área construída, área do terreno, quantidade de quartos e banheiros, quantidade de pavimentos, bairro, etc. A quantidade de características que compõem nossa entrada \(X\) vai depender de diversos fatores, porém principalmente de quais dados conseguimos coletar dentro de um custo-benefício aceitável.
Uma das principais atividades do Cientista de Dados vai ser justamente definir quais características são importantes e relevantes para o que queremos prever, qual o custo e benefício de coletá-las e tentar identificar também variáveis irrelevantes e/ou que acrescentem muito ruído aos dados, mais atrapalhando do que ajudando. A quantidade de características que vamos ter na entrada \(X\) é denotada pela variável \(n\). Podemos dizer que nossa entrada \(X\) é composta por \(n\) características.
Um exemplo, então, vai ser o conjunto de dados de um imóvel em questão. Logo, nós vamos ter todas as características deste imóvel (\(X\)) e o seu preço final (\(y\)). O preço do imóvel (nossa saída \(y\)) neste caso também pode ser chamado de rótulo, que é a resposta da pergunta que queremos responder. Dizemos que são dados rotulados, portanto, sendo um modelo de Aprendizado Supervisionado. Nós fornecemos ao modelo as características (features) e os respectivos rótulos (labels), neste caso os preços.
Nós vamos ter um total de \(m\) exemplos, e o conjunto de todos os exemplos vai ser a nossa base de dados (ou dataset).
Vamos revisar alguns dos termos que vimos até agora.
- \(y \longrightarrow\) saída do modelo, a variável a ser descoberta. Também chamada de variável Alvo / Dependente / Resposta. No nosso caso, o valor do imóvel.
- \(X \longrightarrow\) entrada do modelo, as características a serem usadas para chegar à descoberta. Também chamada de variável Explicativa / Independente / Preditora. Para nós agora, as características do imóvel.
- \(n \longrightarrow\) número de diferentes características disponíveis em uma única entrada.
- \(m \longrightarrow\) número total de exemplos na base de dados sendo usados para treino do modelo.
Regressão Linear
A Regressão Linear é uma forma de identificar uma relação (ou associação) linear entre as características (a entrada \(X\)) e a variável alvo (saída \(y\)).
O algoritmo irá analisar todos os exemplos, com suas respectivas saídas, e buscar padrões que nos retornem um conjunto de regras, uma fórmula matemática, para ser mais exato, para representar o padrão que explica melhor os dados.
Fica mais fácil de entender o conceito visualizando. Nós, seres humanos só conseguimos visualizar dados em até 3 dimensões. Em 1 dimensão nós vamos ter um ponto, em 2 dimensões nós vamos visualizar uma reta, em 3 dimensões um plano e em mais de 3 dimensões teremos hiperplanos, que não podem ser visualizados.
Em nome da didática, vamos usar apenas duas dimensões. Para nosso exemplo de predição de preços de imóveis, vamos levar em consideração por enquanto apenas a área do imóvel (em m²) influenciando no seu valor de mercado.

O algoritmo de Regressão Linear vai buscar a reta que melhor represente a relação entre a área do imóvel e seu valor de mercado. Após analisar todos os exemplos (pontos azuis) o modelo irá retornar para gente a sua fórmula matemática linear que gere a reta mais eficiente para nosso caso.

Vamos lembrar que uma fórmula linear tem a seguinte estrutura.
\[ y = wx + b \]
Até então, neste nosso cenário, temos apenas uma característica, um único \(x\). Temos uma Regressão Linear Simples. Quando temos mais características, teremos mais \(x\)‘s, e, portanto, uma Regressão Linear Múltipla. A estrutura da fórmula de uma Regressão Linear Múltipla com \(nx\) características é a seguinte.
\[y = w_1x_1 + w_2x_2 + w_3x_3 + \dots + w_nx_n + b \]
Em ambos os casos, temos dois parâmetros que precisam ser aprendidos pelo modelo: \(w\) (weight) e \(b\) (bias). Onde \(w\) é o coeficiente angular, ou coeficiente de inclinação da reta, e \(b\) é a constante de intercepto. No caso de apenas uma característica temos apenas um \(w\) e um \(x\), e múltiplas características temos mais de um \(w\) e mais de um \(x\). Note que \(X\) em maiúsculo, como chamamos nossa entrada, é o conjunto de características, e cada característica individual é representada por um \(x\) minúsculo, e o mesmo se aplica para \(W\) e \(w\).
Assim sendo, diferentes combinações de \(w\) e \(b\) nos dão diferentes retas.

Mas como sabemos que a reta vermelha é a melhor reta, a reta que traça a melhor relação entre a entrada e a saída?
Reta de Regressão Linear: a que melhor se ajusta aos dados
A Reta de Regressão (do Inglês, Best Fit Line) é a reta que encontra a relação ideal entre as entradas e saídas de um determinado conjunto de dados. Como vimos, nós podemos ter infinitas retas, porém a reta ideal vai ser a que tem uma menor taxa de erro.
O algoritmo de Regressão Linear executa um procedimento de otimização dos parâmetros \(w\) e \(b\) buscando minimizar o erro da reta a ser traçada. Mas como medimos este erro?
Para calcular o erro da reta em relação a um único ponto, nós medimos a distância vertical entre eles. Se a reta passa exatamente sobre o ponto, a reta acertou na mosca e o erro é zero. Porém se a reta está mil unidades (reais no nosso exemplo) abaixo do ponto, quer dizer que o modelou errou por R$1.000,00 a menos do valor real. Logo, temos 1.000 de erro, ou de residual.
Vamos tentar visualizar a medição do erro de alguns pontos do nosso exemplo.

Nós visualizamos a medida de erro de apenas alguns pontos da nossa base de dados. Mas podemos definir então o erro \(e\) da seguinte forma.
\[ e_i= y_i – \hat{y_i} \]
Onde:
- \(e_i \longrightarrow\) erro (ou residual) no exemplo \(i\).
- \(y_i \longrightarrow\) valor real da saída do exemplo \(i\).
- \(\hat{y_i} \longrightarrow\) valor previsto da saída pelo modelo para o exemplo \(i\).
Basta subtrairmos o valor real de saída do valor que foi previsto pelo modelo e nós teremos assim o erro \(e\), para um único ponto \(i\). Para generalizarmos e termos o erro total, somamos todos os erros de todos os pontos.
\[ \sum e_i \]
Vamos calcular o erro total sobre os erros da amostra que medimos acima.
\[ \sum e_i = 22 + 40 + 16 + 10 + (-42) + (-28) + (-20) = -2 \]
Podemos notar que tivemos bastante erro, mas ainda assim o nosso resultado final foi apenas \(-2\)! E isso acontece por termos erros acima e abaixo da reta, em sentidos opostos, que acabam se cancelando. Para evitar isso, nós podemos elevar cada uma dessas diferenças, cada um desses valores, ao quadrado.
\[ \sum e_i = 22^2 + 40^2 + 16^2 + 10^2 + (-42)^2 + (-28)^2 + (-20)^2 \]
\[ \sum e_i = 484 + 1600 + 256 + 100 + 1764 + 784 + 400 = 5388 \]
Agora sim, nós temos um erro de \(5388\), que é muito mais relevante. O algoritmo de Regressão Linear vai fazer uso de um algoritmo de optimização, como o Gradiente Descendente Estocástico (provavelmente falaremos sobre isso num post futuro), para encontrar a reta que leva a este menor erro.
Podemos definir este erro como a Soma dos Quadrados das Diferenças os valores reais e os valores previstos pelo modelo. E teremos a seguinte fórmula para calculá-lo.
\[ \sum e_i^2 = (y_i – \hat{y}_i)^2\]
Ótimo! Agora sabemos encontrar a melhor reta… A reta que tem a menor taxa de erro quadrático. Mas o quão boa essa reta é de fato?
Medidas de Eficiência da Regressão Linear
Também chamadas de Medidas de Ajuste de Regressão, são métricas para nos dizer o quanto um modelo de Regressão Linear é preciso, ou seja, o quanto ele é capaz de explicar os dados observados.
Após encontrarmos a melhor reta para nossa distribuição de dados, é muito importante sabermos o quão boa essa reta de fato é para predizer valores futuros. Muitas vezes a “melhor” não quer dizer que seja boa o suficiente.

Vocês concordam que acima temos nos dois casos a melhor reta para a distribuição dos dados? Mas concordam também que no caso da direita vamos ter uma taxa de acerto muito maior? Ou seja, vamos ter uma reta com uma eficiência muito maior que a outra.
Existem diversas medidas de eficiência diferentes, cada uma delas com suas particularidades e propriedades. Vamos ver aqui algumas das medidas mais comuns.
Coeficiente de Determinação (R²)
É provavelmente a métrica mais comum e mede a proporção da variação dos dados observados que é explicada pelo modelo. Ele é definido pela seguinte fórmula.
\[ R^2 = 1 – \frac{\sum e_i^2}{\sum (y_i – \bar{y})^2} \]
Um termo novo desta fórmula que ainda não vimos é o \(\bar{y}\) (ípsilon barra), que é a média dos valores reais de \(y\). Se nós não tivermos nenhum erro, ou residual zero (\(\sum e_i^2 = 0\)), então isso significa que nós conseguimos explicar 100% dos dados com nosso modelo. Então temos que R² é igual a 1, ou seja, 100% de acertos do modelo.
Se os valores residuais, erros, forem iguais à variância ( \(\sum e_i^2 = \sum (y_i – \bar{y})^2\) ), significa que não conseguimos explicar nada com o modelo, 0%. Com isso, nosso R² vai ser igual a 0.
De forma resumida, o R² varia entre 0 e 1. Quanto mais próximo de 1, melhor o modelo, e quanto mais próximo de 0, pior.
Erro Médio Absoluto (MAE)
O Erro Médio Absoluto (Mean Absolute Error, ou MAE) faz uso dos valores absolutos (em módulo) dos erros que calculamos como no exemplo acima. O uso do valor absoluto evita que os erros se cancelem, deixando todos com sinal positivo. Somamos todos os valores absolutos das diferenças da regressão e dividimos pelo total de \(m\) exemplos, para termos a média.
\[ \text{MAE} = \frac{\sum |e_i|}{m} = \frac{ \sum |y_i – \hat{y_i} |}{m} \]
Esta é uma métrica bem simples para verificar a acurácia do modelo. Ela é medida na mesma unidade da variável dependente e não é sensível a outliers, ou seja, valores muito extremos não vão impactar esta métrica em uma escala intensificada.
Quanto menor o MAE, melhor.
Erro Médio Quadrático (MSE)
O Erro Médio Quadrático (Mean Squared Error, ou MSE) é bem similar ao cálculo de erro, a soma dos quadrados das diferenças da regressão. A diferença é que dividimos o erro total pela quantidade \(m\) de exemplos, para termos a média.
\[ \text{MSE} = \frac{ \sum e_i^2}{m} = \frac{ \sum (y_i – \hat{y_i} )^2}{m} \]
Esta é uma outra métrica para medir a acurácia do nosso modelo. Neste caso, a métrica é muito mais sensível a outliers, ou seja, valores extremos vão ter um peso muito maior no valor de erro final. Essa é uma métrica muito boa para quando precisamos punir erros muito grotescos.
Caso errar por pouco ou errar por muito não faça diferença para nosso objetivo, MAE pode ser uma boa métrica. Agora se errar por muito fizer bastante diferença, MSE é a métrica a ser escolhida.
Quanto menor o MSE, melhor.
Raiz do Erro Médio Quadrático (RMSE)
A Raiz do Erro Médio Quadrático (Root Mean Squared Error, ou RMSE) é basicamente a raiz quadrada do MSE descrito acima. É muito útil quando os erros da previsão do modelo são expressos em uma unidade diferente daquela dos dados observados.
\[ \text{RMSE} = \sqrt{\frac{ \sum e_i^2}{m}} = \sqrt{\frac{ \sum (y_i – \hat{y_i} )^2}{m}} \]
Por tirar a raiz quadrada do MSE, ela penaliza os erros de forma menos severa e traz para valores mais baixos para a taxa de erro, retirando o fator exponencial.
Quanto menor o RMSE, melhor.
Prevendo valores futuros
Uma vez que alimentamos nosso modelo de Regressão Linear com nossos exemplos, nossa base de treino, ele roda seu algoritmo de otimização para convergir para os parâmetros \(w\) e \(b\) que nos dão o menor erro, encontrando assim a Reta de Regressão, ou a melhor reta. Reta esta que vai ser representada por uma fórmula matemática no formado: \(y = wx + b\)
Analisamos as métricas de eficiência desta reta encontrada para ver se temos uma performance aceitável com esse nosso modelo treinado. Bons resultados tendo sido atingidos, validamos nosso modelo como bom para uso e podemos começar a fazer nossas predições de valores futuros.
Para isso, basta pegarmos o(s) valor(es) de \(x\) e multiplicar pelo(s) parâmetro(s) \(w\) e somar com \(b\). Isso vai nos dar a previsão do modelo, o que chamamos de \(\hat{y_i}\) (ípsilon hat).
Novamente pelo bem da didática, vamos supor que temos os seguintes exemplos na nossa base de treino para a geração de uma Regressão Linear genérica.
| X | y |
|---|---|
| 0 | 200.0 |
| 1 | 202.5 |
| 2 | 205.0 |
| 3 | 207.5 |
| 6 | ? |
Para os exemplos acima encontramos os valores de \(w = 2,5\) e de \(b = 200\), e para encontrar cada valor de saída \(y\), basta multiplicarmos o valor de \(x\) por \(w\) (ou \(2,5\)) e somar com \(b\) (ou \(200\)).
Supondo que o valor futuro que queremos prever, o valor que a regressão ainda não viu, é o valor de \(x = 6\), aplicaremos a fórmula.
\[ y = wx + b = 2.5 * 6 + 200 = 215 \]
Podemos visualizar graficamente também a predição de novos valores como seria.
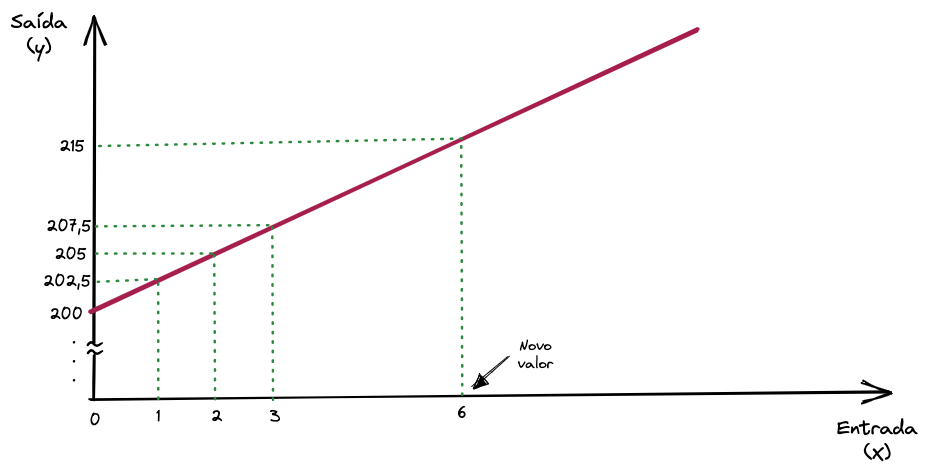
Note que o valor de \(b\) é onde a reta intercepta o eixo y.
O mesmo princípio e processo são aplicados para qualquer regressão, inclusive para o nosso exemplo onde tentamos prever os valores dos imóveis.

Qualquer novo valor antes não visto pelo modelo no eixo x pode ser mapeado por esta reta para seu respectivo valor no eixo y.
O mesmo se aplicaria no caso de uma regressão múltipla, com \(n\) características. Teríamos \(x_n\) características e \(w_n\) parâmetros para serem aprendidos. A única diferença é que nós, humanos, não conseguiríamos facilmente visualizar isso em gráfico.
Vantagens e Desvantagens da Regressão Linear
A Regressão Linear é provavelmente hoje o modelo mais utilizado do mundo. É um modelo simples e elegante que oferece uma performance computacional extremamente eficiente.
É uma solução útil quando temos uma relação linear entre a entrada e a saída do modelo, variáveis explicativas e variável alvo. E também é um modelo que oferece uma alta explicabilidade, pois é fácil de se interpretar os coeficientes da regressão e entender cada decisão tomada pelo modelo.
Em contrapartida, é muitas vezes um modelo simples demais para capturar as complexidades do mundo real. Nem sempre teremos uma relação linear entre as variáveis. O modelo também assume algumas premissas que nem sempre são verdadeiras para dados reais, como a independência entre as características.
Sem dúvidas, apesar da simplicidade, é uma ferramenta importantíssima para se ter na nossa caixa de ferramentas e que pode ser usada para suportar modelos mais complexos e robustos. Além, é claro, de servir como base teórica para entendermos outros algoritmos.
Conclusão
Como sempre, nosso objetivo é instigar a curiosidade de vocês. Queremos permitir que deem os primeiros passos em direção a este mundo fascinante do Machine Learning. Se você se interessou ainda mais sobre o assunto, nosso objetivo foi alcançado.
É possível ver exemplos práticos de como desenvolver uma Regressão Linear em código. Você pode acessar nosso post Prática: Regressão Linear, com código em Python.
Existem muitas outras regressões, mais complexas, e que capturam mais as particularidades de dados do mundo real, como as Regressões Polinomiais. Temos também as Regressões Lasso e Ridge. Se você tiver interesse, vale a pena pesquisar sobre elas. Em breve falaremos sobre outras formas de regressão aqui no BRAINS.
Caso tenha ficado com dúvidas e queira trocar uma ideia, deixa um comentário que com certeza iremos responder. Se você dominar algumas outras formas de regressão (ou outros temas) e quiser colaborar com a nossa comunidade escrevendo para o BRAINS, entre em contato com a gente. E se você ainda não domina, mas está estudando (provavelmente consumindo conteúdo em Inglês), você também pode colaborar com nossa comunidade traduzindo conteúdo ou gerando o seu próprio em Português enquanto estuda.
De toda forma, não deixe de conhecer mais sobre o BRAINS – Brazilian AI Networks. A comunidade de estudantes tem como objetivo trazer conteúdo de qualidade sobre AI, Dados e ML para Brasileiros, em Português.
Happy codding! 🙂




3 comentários