É indispensável medirmos a performance, ou eficiência, dos nossos modelos de Machine Learning. Nós buscamos a princípio construir o melhor modelo possível sobre os nossos dados, minimizando o erro (ou perda). Porém, precisamos saber quão bom “o melhor” é. Para isto, iremos conhecer algumas métricas e técnicas.

Sabemos que nossos modelos de classificação – vamos continuar exemplificando sobre a Classificação Binária – podem errar e podem acertar nas suas predições após aprender sobre a nossa base de treino. Porém, os modelos podem errar e acertar de formas diferentes. Vamos ver como.
Se por acaso você está confuso com os termos “Modelo de Classificação”, “Classificação Binária”, “perda” e “base de treino”. Recomendamos a leitura de dois posts aqui no BRAINS. O Primeiramente, o que é Machine Learning? é mais introdutório e generalista, é um ótimo ponto de partida. No post Modelos de Classificação: Regressão Logística nós vamos um pouco mais a fundo em como um algoritmo de classificação funciona.
É muito importante ressaltar que não importa qual algoritmo de Classificação você está usando, os conceitos aqui apresentados se aplicarão a todos. Pode ser Machine Learning clássico, Deep Learning, Visão Computacional, Classificação de Texto ou qualquer outro. As medidas de performance e técnicas serão as mesmas.
Machine Learning Crash Course, por Google Developers
Muitos dos exemplos usados aqui foram construídos com base no curso Machine Learning Crash Course disponibilizado, em Inglês, pelo Google Developers.
Fonte: https://developers.google.com/machine-learning/crash-course
Vamos lá!
Como Modelos de Classificação aprendem?
É importante relembrarmos como os modelos de classificação aprendem. Modelos de classificação são um formato de Aprendizado de Máquina Supervisionado, então nós precisamos fornecer para o modelo uma série de exemplos, com suas respectivas saídas.
Os exemplos fornecidos são os nossos dados, e para cada exemplo – cada linha da base de dados – temos uma série de características – colunas da base de dados. Um único exemplo nós chamamos de \(x_{i}\), onde \(i\) representa o número desse exemplo. \(x_{i}\) é um vetor com os valores das suas características. O conjunto de todos os exemplos chamamos de \(X\), uma matriz com todos os valores de características de todos os exemplos.
Como sabemos, para cada exemplo (e suas características) precisamos saber o valor real da sua respectiva saída. Quando temos as saídas de cada um dos exemplos, dizemos que os dados são rotulados. Portanto, podemos chamar a saída de rótulo. Chamamos o conjunto de rótulos de \(y\), um vetor com os valores reais das saídas de cada exemplo. Em uma classificação binária os valores do vetor \(y\) serão uma cadeia de True e False, ou 1s e 0s.
Uma coisa é a saída real (que em Inglês costumamos chamar de Ground Truth), ou rótulo, \(y\). Outra coisa é a predição do modelo, ou \(\hat{y_{}}\) (“ípsilon hat”). Nós esperamos que a predição do modelo \(\hat{y_{}}\) seja igual ao valor real \(y\), ou o mais próximo possível disto.
Quanto mais próximo \(\hat{y_{}}\) está de \(y\), melhor o modelo. É comparando estes dois valores que medimos o erro, ou a perda, e como verificamos se o modelo acertou ou errou.
TP, TN, FP, FN, WTF ?
Se você já leu sobre modelos de Machine Learning classificando suas entradas, provavelmente já se deparou com as siglas TP, TN, FP, FN, mas… what the f*ck?
Em uma (educada) tradução: o que seria isto?
Essas quatro siglas representam as quatro formas em que os nossos modelos podem acertar e errar. T vem de True, ou verdadeiro. F vem de False, ou falso. P vem de Positive, positivo. E N de Negative, negativo. As quatro letras formam essas quatro combinações.
Para simplificar o entendimento, podemos notar que tudo que começa com True (T) é um acerto do modelo. True Positive (TP) o modelo previu que a classe era positiva e de fato ela era. True Negative (TN) o modelo previu que a classe era negativa, e de fato era.
Tudo que começa com False (F) é um erro do modelo. False Positive (FP) o modelo previu que a classe era positiva, mas na verdade ela era negativa. False Negative (FN) o modelo previu que a classe era negativa, porém era positiva.
Resumindo e estruturando melhor:
- True Positive (TP): Verdadeiro Positivo, um acerto! O modelo prevê corretamente a classe positiva.
- True Negative (TN): Verdadeiro Negativo, um acerto! O modelo prevê corretamente a classe negativa.
- False Positive (FP): Falso Positivo, um erro! O modelo prevê incorretamente a classe positiva.
- False Negative (FN): Falso Negativo, um erro! O modelo prevê incorretamente a classe negativa.
Obviamente, para sabermos os erros e acertos precisamos comparar o valor da predição do modelo ( \(\hat{y_{}}\) ) com o rótulo, ou o valor real de saída ( \(y\) ).
Vamos ver uma forma melhor – gráfica – de analisar as taxas de erros e acertos.
Matriz de Confusão
Apesar da “confusão” no nome, é bem simples de se entender este conceito. A Matriz de Confusão (Confusion Matrix) nada mais é do que a representação tabular das Classes Previstas vs Classes Reais. Ou seja, \(\hat{y_{}}\) vs \(y\).
Graficamente ficará muito mais fácil.
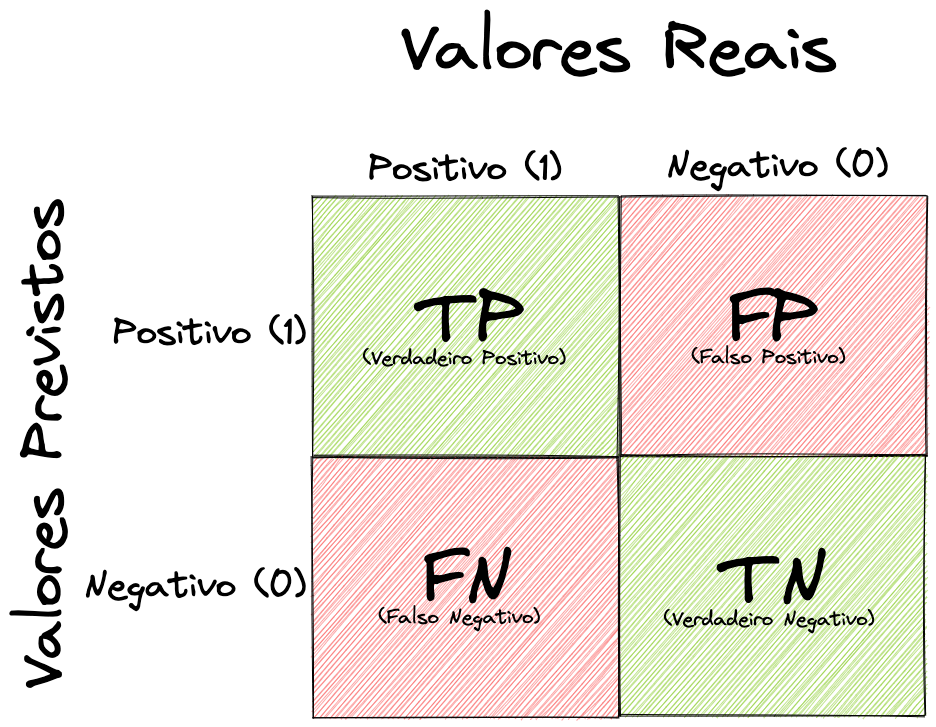
No eixo X (horizontal) nós temos os Valores Reais \(y\), os rótulos verdadeiros da nossa base de treino. No eixo Y (vertical) temos os Valores Previstos \(\hat{y_{}}\), a predição do nosso modelo.
Podemos reparar que os quadrantes dos acertos, os que começam com T, estão destacados em verde. Os quadrantes dos erros, começam com F, estão em vermelho.
Para sabermos se o modelo acertou ou errou, precisamos verificar se o valor previsto é igual ao valor real. Se forem iguais, o modelo acertou. Perceba que 1 com 1 é um acerto da classe positiva e 0 com 0 é um acerto da classe negativa. Por outro lado 1 com 0 e 0 com 1 representam erros.
Agora que sabemos como definir diferentes tipos de erros e acertos, você pode estar se perguntando: um tipo de erro pode ser pior que o outro?
Se você se perguntou isso, parabéns! Dependendo da aplicação do nosso modelo de Machine Learning, um erro pode ser muito pior do que o outro sim. Mas adiante vamos ver isso com mais detalhes.
Antes, porém, vamos ver como converter essa sopa de letrinhas de Ts, Fs, Ps e Ns em métricas de fato, em valores.
Acurácia de um modelo
A Acurácia (Accuracy) é provavelmente a forma mais intuitiva de se medir a performance do modelo. É só vermos, de todos os exemplos que temos, quantos ele acertou. Se fornecemos 100 exemplos e o modelo acertou 90, temos uma Acurácia de 90/100. Ou seja, 90%.
Informalmente, podemos definir a Acurácia desta forma mesmo, como a proporção das predições que o nosso modelo acertou. Mais formalmente, definimos a Acurácia como a relação entre o número correto de predições sobre o total de predições feitas.
\[ \text{Acurácia} = \frac{\text{Qtd Predições Corretas}}{\text{Qtd Total de Predições}} \]
Agora que nós já dominamos as siglas de erros e de acertos, podemos melhorar esta fórmula.
\[ \text{Acurácia} = \frac{TP + TN}{TP + TN + FP + FN} \]
Fica bem fácil de associarmos. Sabemos que tudo que começa com T é um acerto, logo para termos o total de acertos basta somarmos TP (os acertos de Verdadeiro Positivo) com TN (os acertos de Verdadeiro Negativo). Somamos os dois quadrantes verdes, de acertos. Dividimos agora este valor pelo total de predições
Para termos o total de predições, precisamos somar todos os erros e todos os acertos. Ou seja, somamos os valores dos quatro quadrantes: TP, TN, FP e FN.
Bem intuitivo e fácil de entender. Mas será que podemos usar sempre a Acurácia?
Acurácia é a melhor métrica?
A resposta para esta pergunta é a mesma para quase tudo que podemos perguntar sobre aplicação de Machine Learning: DEPENDE!
Esta métrica é sem sombra de dúvidas uma ótima medida de performance e nos dá uma informação importante. A Acurácia sozinha, porém, pode não contar a história por completo.
Para fins didáticos e de exemplificação, vamos supor que nós estamos construindo um modelo para prever se um tumor é maligno (classe Positiva 1) ou benigno (classe Negativa 0). Suponhamos que nossa base de treino tenha 100 exemplos, onde 91 são benignos (classe Negativa 0) e 9 tumores são malignos (classe Positiva 1).
\[ \left. \begin{array}{cl}
91 \text{ Negativo, classe } 0 \text{ (benigno)}\\
09 \text{ Positivo, classe } 1 \text{ (maligno)}
\end{array} \right\} \to \text{Total de } 100 \text{ exemplos} \]
Treinamos o nosso modelo sobre os 100 exemplos e na hora de avaliá-lo temos a seguinte Matriz de Confusão.

Parece que acertamos bastante. Vamos calcular a Acurácia?
\[ \text{Acurácia} = \frac{TP + TN}{TP + TN + FP + FN} = \frac{1 + 90}{1 + 90 + 1 + 8} = 0.91 \]
Temos uma Acurácia de 91%, pois acertamos 91 predições de um total de 100 exemplos. Parece muito bom o nosso modelo, certo? Errado.
Vamos olhar um pouco mais de perto os erros do nosso modelo.
Do ponto de vista do cliente
É muito importante, como Cientistas de Dados, nos colocarmos no lugar do nosso cliente e analisar onde podem haver perdas maiores. O nosso cliente, nesse exemplo, seria o médico, que faz uso de um modelo de Machine Learning para auxiliá-lo nas tomadas de decisão. Tendo em mãos um modelo com 91% de acerto, o médico consegue dar foco maior nos pacientes críticos.
Então, um tumor que tem como resultado a classe 0, benigno, o médico analisa e encaminha o paciente para o tratamento adequado (mais leve talvez). Um tumor com o resultado de classe 1, maligno, é alarmante para o médico, que precisa tomar providências mais emergenciais e encaminhar o paciente para um tratamento mais intensivo (supondo, para fins didáticos, não domino o assunto).
Voltando à análise do nosso modelo, dos 100 exemplos de tumores, 91 eram benignos (classe Negativa 0): acertamos 90 como TNs e erramos 1 como FP. Apenas 9 tumores eram malignos (classe Positiva 1): acertamos 1 TP e erramos 8 FNs. Verifique novamente na Matriz de Confusão acima se estiver com dúvidas.
Dos 91 tumores benignos, o modelo conseguiu prever corretamente 90 como benignos e isso é bom. Entretanto, dos 9 tumores malignos, o modelo conseguiu identificar apenas 1! Um resultado terrível. 8 das 9 pessoas com tumores malignos não foram diagnosticadas corretamente pelo modelo.
Este modelo precisaria ser revisado com urgência.
Um exemplo mais simples
Vamos levar este exemplo um pouco além e supor que temos uma nova base de dados para treino, novamente com 100 exemplos. Temos desta vez, porém, apenas 2 exemplos de tumores malignos e 98 exemplos de tumores benignos.
Não precisamos sequer desenhar uma Matriz de Confusão para ver como a Acurácia pode nos enganar. Se o nosso modelo for treinado focando em melhorar a Acurácia, este modelo pode simplesmente “chutar” sempre que todos os tumores são benignos e ainda assim vai ter uma Acurácia de 98%. Afinal de contas, ele vai ter acertado os 98 benignos dos 100 exemplos.
O mesmo se aplicaria ao exemplo anterior, com 91 benignos e 9 malignos. Se o modelo previsse todos como benignos, teria a mesma Acurácia de 91%.
Como dito, a Acurácia nem sempre conta toda a história e pode nos enganar. Principalmente em bases de dados de treino desbalanceadas, ou seja, onde há uma disparidade muito grande entre as duas classes, onde uma classe é dominante.
Para sabermos a história completa, precisamos de outras métricas para complementar a Acurácia.
Precisão
Começaremos a ver os outros lados da história agora. A Precisão (Precision) é definida como a fração dos resultados positivos corretos em relação a todos os resultados positivos produzidos pelo modelo. A pergunta que Precisão tenta responder é:
- Qual a proporção de predições positivas que estavam realmente corretas?
Ou seja, queremos as predições positivas corretas (TP) sobre todas as predições do modelo da classe positiva, tanto as predições que o modelo acertou predizendo positivo (TP) quando errou predizendo positivo (FP). Podemos colocar isso também em uma fórmula.
\[ \text{Precisão} = \frac{TP}{TP + FP} \]
Novamente, Precisão é a razão entre o número de Verdadeiros Positivos (TP) e o número total de positivos preditos pelo modelo, incluindo erros e acertos (TP + FP).
Exemplificaremos usando o mesmo exemplo acima, predição de tumores. Continuaremos com 100 exemplos de tumores, onde 91 são benignos (classe Negativa 0) e 9 são malignos (classe Positiva 1). Vamos ver novamente a sua Matriz de Confusão.

Vamos extrair os valores de Verdadeiros Positivos (TP) e de Falsos Positivos (FP) para aplicar na nossa fórmula.
\[ \text{Precisão} = \frac{TP}{TP + FP} = \frac{1}{1 + 1} = 0.5 \]
Nosso modelo tem uma Precisão de 0.5. Em outras palavras, quando ele prevê que um tumor é maligno (classe Positiva 1), ele está correto 50% das vezes.
Recall
O termo Recall costuma ser encontrado de diferentes formas na literatura brasileira. Há quem chame de Revocação, Taxa de Cobertura, Taxa de Captura, e até de Sensibilidade já vi gente chamando. Confesso que não sei a melhor tradução, portanto iremos chamar aqui de Recall mesmo, ok?
A definição de Recall pode ser como a fração dos resultados positivos corretos em relação a todos os resultados positivos reais. A pergunta que Recall tenta responder é:
- Qual a proporção de valores positivos que foi identificada corretamente?
Dentre todos os exemplos positivos, onde o valor real é a classe 1, quantos o meu modelo acertou? Ou seja, queremos as predições positivas corretas (TP) sobre todos os exemplos positivos, e a forma de encontrarmos todos os exemplos positivos é verificando onde o modelo acertou como positivo (TP) e onde ele errou achando que era negativo (FN) mas de fato era positivo.
Segue a fórmula.
\[ \text{Recall} = \frac{TP}{TP + FN} \]
Podemos dizer que Recall nos diz quantos dos resultados positivos em um conjunto de exemplos o modelo foi capaz de capturar (talvez daí o nome Taxa de Captura). Novamente, Recall é a razão entre os Verdadeiros Positivos (TP) e todos os exemplos verdadeiros da base de dados, incluindo os que o modelo acertou dizendo positivo e errou dizendo negativo (TP + FN).
Vamos usar o mesmo exemplo para calcular o Recall e deixar aqui abaixo a Matriz de Confusão novamente para facilitar.

Extraindo os valores e aplicando a fórmula, teremos:
\[ \text{Recall} = \frac{TP}{TP + FN} = \frac{1}{1 + 8} = 0.11\]
Temos um Recall de 0.11 apenas. Isso quer dizer que o modelo só identifica corretamente 11% dos tumores malignos.
Cabo de Guerra: Precisão vs Recall
Se analisarmos bem, iremos perceber que quando um modelo foca em ter uma Precisão maior, ele diminui os erros de Falso Positivos (FP), e quando o modelo foca em ter um Recall maior, ele diminui os erros de Falso Negativos (FN).
- Um modelo que não produz nenhum Falso Positivo (FP) tem uma Precisão de \(1.0\), ou 100%.
- Um modelo que não produz nenhum Falso Negativo (FN) tem um Recall de \(1.0\), ou 100%.
Infelizmente estas duas métricas estão normalmente sob tensão. Isso quer dizer que na maioria das vezes, ao aumentarmos a Precisão nós diminuímos o Recall e vice-versa. Não vamos apenas falar isso, vamos provar, com um exemplo.
Iremos revisitar o nosso exemplo de um modelo classificador de spam que usamos no post Modelos de Classificação: Regressão Logística. Para simplificar, vamos compactar os dados em um único eixo horizontal, que vai ser o resultado da Regressão Logística, que sabemos que são valores entre 0 e 1.
Vamos analisar melhor essa nova visualização de dados.

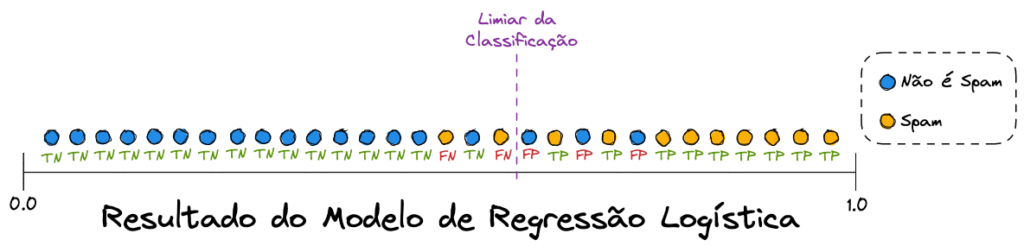
Como falamos, estamos visualizando os dados binários sob um único eixo horizontal. O que representa o eixo vertical são as cores dos pontos: azul representa a classe 0 (não spam) e amarelo representa a classe 1 (spam). A nossa linha tracejada roxa é o nosso limiar da classificação (leia o post recomendado caso não tenha entendido). Então tudo à esquerda do limiar o modelo previu como classe 0 (não spam) e tudo à direita ele previu como classe 1 (spam).
Analisando os resultados do modelo de Spam
Note que o modelo errou, para os dois lados. Tudo que é azul e está à esquerda do limiar é um acerto de TN (Verdadeiro Negativo), porém o que é amarelo e está à esquerda é um erro de FN (Falso Negativo)
Tudo que é amarelo e está à direita do limiar foi classificado corretamente como spam, ou seja, são TP (Verdadeiro Positivos). Entretanto, o que é azul e está à direita do limiar foi incorretamente classificado como spam, então cada ponto deste trata-se de um FP (Falso Positivo).
Repare que deixamos as siglas dos acertos em verde sob os pontos e as dos erros em vermelho, para facilitar o entendimento.
Vamos desenhar a Matriz de Confusão deste modelo para visualizar melhor.

Repare que nós temos 30 exemplos de emails. 11 são de fato spam (coluna da esquerda da matriz) e 19 não são spam (coluna da direita da matriz). Analise a visualização dos dados acima e esta Matriz de Confusão, esta é uma oportunidade bacana para internalizar este conhecimento. Recomendamos seguir com a leitura só depois que tiver entendido de fato como chegamos até aqui.
Calcularemos a Precisão e o Recall agora.
Precisão irá medir a porcentagem de e-mails classificados como spam que foram corretamente classificados, ou seja, a porcentagem de pontos amarelos dentre os pontos à direita do limiar.
\[ \text{Precisão} = \frac{TP}{TP + FP} = \frac{8}{8 + 2} = 0.8 \]
Recall irá medir a porcentagem de spams que foram corretamente classificados, ou seja, a porcentagem de pontos amarelos que estão à direita do limiar dentre todos os pontos amarelos.
\[ \text{Recall} = \frac{TP}{TP + FN} = \frac{8}{8 + 3} = 0.73\]
Aumentando o limiar
Supondo que achamos que o nosso modelo tem classificado e-mails importantes demais como spam. Isso quer dizer que ele tem uma taxa alta de Falso Positivo (FP) e queremos diminuir esta taxa.
Para diminuir esta taxa, como sabemos, precisamos focar em aumentar a nossa Precisão. E para aumentar a Precisão, podemos mover o nosso limiar mais para a direita. Vamos visualizar novamente como ficam as classificações agora.

Ajustamos o limiar para diminuir os Falso Positivos (FP). Desenharemos a nova Matriz de Confusão.

Vamos analisar como a Precisão e Recall se comportam.
\[ \text{Precisão} = \frac{TP}{TP + FP} = \frac{7}{7 + 1} = 0.88 \]
\[ \text{Recall} = \frac{TP}{TP + FN} = \frac{7}{7 + 4} = 0.64\]
Aumentamos a Precisão para melhorar (diminuir) a taxa de Falso Positivos (FP), porém para isso tivemos que sacrificar um pouco do Recall e pioramos (aumentamos) a taxa de Falso Negativos (FN).
Diminuindo o limiar
Agora vamos fazer o oposto. Supondo que achamos que o classificador de spam está deixando muito spam passar para a nossa caixa de entrada, ou seja não está classificando corretamente que um spam é um spam. Em outras palavras, está dando um resultado negativo para um e-mail que é positivo para spam. Logo, estamos com uma taxa alta de Falso Negativos (FN).
Sabemos que precisamos aumentar o Recall para diminuir os Falso Negativos. Para melhorar o Recall iremos mover o nosso limiar para a esquerda. Vamos visualizar novamente nossos dados.
Desta vez ajustamos o limiar para diminuir os Falso Negativos (FN). Novamente desenharemos a Matriz de Confusão atual.

Perceba que desta vez conseguimos fazer com que os Falso Negativos (FN) diminuam, mas os Falso Positivos (FP) aumentaram. Vamos recalcular Precisão e Recall.
\[ \text{Precisão} = \frac{TP}{TP + FP} = \frac{9}{9 + 3} = 0.75 \]
\[ \text{Recall} = \frac{TP}{TP + FN} = \frac{9}{9 + 2} = 0.82\]
Alcançamos nosso objetivo de aumentar o Recall, o que melhorou (diminuiu) a taxa de Falso Negativo (FN). Em contrapartida, isso nos levou a diminuir a Precisão, piorando (aumentando) a taxa de Falso Positivo (FP).
Perceberam o cabo de guerra?
A História Completa
Conseguimos perceber que para uma avaliação completa do modelo precisamos das três métricas: Acurácia, Precisão e Recall. Além disso, a Matriz de Confusão nos ajuda a entender melhor os erros e acertos dos nossos modelos.
Voltando à pergunta “um tipo de erro pode ser pior que o outro?” e indo um pouco além, pois agora vocês podem estar se perguntando: “já que não posso ter os dois, é melhor focar na Precisão ou Recall?”
Novamente, a resposta é a mais fácil e mais difícil de se dar: DEPENDE!
Para contar a história completa do nosso modelo e podermos definir qual métrica é mais importante. Para algumas aplicações, como a do câncer, fica óbvio que um tumor maligno não identificado (FN) teria consequências muito maiores do que um tumor benigno que foi apontado como maligno (FP). É melhor darmos atenção demais a um benigno do que de menos a um tumor maligno, concordam?
Mas vamos usar um outro exemplo, menos óbvio, e mais próximo da realidade dos negócios. Suponhamos que nós somos Cientistas de Dados trabalhando para uma empresa financeira que possui um ótimo histórico de clientes que aceitaram e recusaram empréstimos no passado. Essa empresa quer nos contratar para criar um modelo para prever clientes propensos a aceitar empréstimos no futuro.
Entendendo o contexto
Antes de começar a construir qualquer modelo de Machine Learning, precisamos entender o contexto da empresa e do negócio. Só assim conseguiremos construir algo que de fato entregue valor.
Essa empresa, nosso cliente, faz uso do telemarketing para abordar os seus clientes e oferecer empréstimos. Hoje eles possuem um catálogo de milhões de pessoas para serem abordadas com ofertas de empréstimo. Porém, fazer isso sem um embasamento é como “dar tiros no escuro”. A empresa possui uma equipe de análise de clientes, mas o processo é muito lento e manual, e leva a muitos erros. Por isso decidiram recorrer à Inteligência Artificial.
Nosso objetivo como Cientistas de Dados é pegar os milhões de possíveis clientes e classificá-los como propensos a aceitar um empréstimo (classe 1) ou não propensos a aceitar (classe 0). Desta forma a empresa poderá ligar apenas para os clientes mais propensos, canalizando os investimentos e aumentando o seu ROI (Return On Investment, ou Retorno sobre Investimento).
Não iremos entrar nos detalhes da construção do modelo, Matriz de Confusão e nem calcular as métricas. Já fizemos isso o suficiente. O ponto é que chegamos em um bom modelo, aceitável, mas que encontra-se na mesma situação do de spam. Precisamos tomar a decisão de melhorar a Precisão ou melhorar o Recall. E qual dos dois melhorar? A decisão não é mais tão óbvia.
Bom, a resposta é que isso vai depender do momento negocial do cliente (sempre depende, né? haha). O que eu quero dizer com isso? Analisemos o contexto, a história completa.
Falamos que a empresa faz contato com seus clientes via telefone. Logo, sabemos que cada ligação tem um custo e que os recursos são limitados, certo? Vamos analisar as possibilidades.
Foco na Precisão
Em um momento onde a empresa precisa cortar custos, nós podemos focar em aumentar a Precisão, diminuindo assim a taxa de Falso Positivo (FP). O que irá acontecer neste cenário é que o modelo vai ficar mais criterioso, só classificando clientes como propensos a aceitar um empréstimo quando de fato houver uma probabilidade alta de isto acontecer.
Desta forma, quando a empresa ligar para as pessoas, vai haver uma taxa menor de recusa do empréstimo, o que possivelmente vai aumentar o indicador de porcentagem de conversão. Isso acontece pois o modelo não classifica mais tanto clientes como propensos quando de fato não estão.
Por outro lado, o modelo vai deixar de identificar pessoas que aceitariam um empréstimo, pois vão ter diversos propensos sendo classificados como não propensos (FN).
Foco no Recall
Com o passar do tempo, a empresa tem mais recursos para investir na abordagem dos clientes e decide mudar a estratégia. Agora eles querem identificar o máximo de pessoas propensas a pegar um empréstimo, mesmo que isso custe algumas ligações sem sucesso. Para fazer isso, precisamos aumentar o Recall e diminuir as taxas de Falso Negativos (FN).
Assim o nosso modelo ficará um pouco menos criterioso e com certeza classificará algumas pessoas como propensas ao empréstimo mesmo sem elas serem. Porém, vamos capturar uma fatia muito maior das pessoas de fato propensas a pagar.
O custo disso vai ser uma taxa maior de Falso Positivos (FP), o que significa a empresa ligando para pessoas classificadas como propensas, mas que no final não aceitam o empréstimo.
Viram como é verdade quando falamos que “depende”?
Equilíbrio: Precisão & Recall ⚖️
Ok, existem situações que não é possível dar preferência a uma métrica sobre a outra. Então o que fazemos quando precisamos equilibrar Precisão e Recall e focar nas duas ao mesmo tempo?
Temos algumas opções.
A primeira acredito que muitos de vocês já tenham até imaginado, que é trabalhar com o limiar do nosso modelo. Vimos acima que ao alterarmos o limiar nós alteramos também essas métricas e as taxas de erros.
Podemos trabalhar sobre o limiar de classificação do modelo para encontrar um equilíbrio entre as duas métricas. Vamos ver um exemplo.

Plotamos no gráfico acima as curvas da Precisão e do Recall em função do Limiar de Classificação do modelo. Isso nos mostra que com o limiar em torno de 0.6 nós temos um equilíbrio entre as duas métricas (0.58 para ser mais exato).
Com isso conseguimos encontrar um limiar “ideal” para equilibrar o modelo. A palavra “ideal” está entre aspas pois obviamente isso nunca será argumento para que este limiar encontrado seja escolhido ao invés de um limiar que faça mais sentido pro negócio final do modelo.
F1-Score
O F1-Score também é conhecido como F-score e F-measure e pode ser traduzido como “Medida F1”. É uma métrica que leva em consideração ambos, Precisão e Recall. Pode ser usado muitas vezes como uma forma de buscar equilíbrio entre as duas ou até mesmo como uma única métrica a ser analisada ao invés de duas (porém lembre-se de sempre avaliar a história completa).
O F1-Score nada mais é do que a média harmônica da Precisão e do Recall. Assim sendo, ele leva em consideração tanto os erros de Falso Positivos (FP) quanto os de Falso Negativos (FN). A fórmula do F1-Score é a seguinte.
\[ \text{F1-Score} = \frac{2 * \text{Precisão} * \text{Recall}}{\text{Precisão } + \text{Recall}} \]
O maior valor possível para o F1-Score é \(1.0\), indicando Precisão e Recall perfeitos, e o valor mínimo possível é \(0.0\).
Conclusão
Eu juro que imaginei que este post seria mais curto, mas ao que tudo indica ele foi o mais longo que já escrevi até agora aqui para o BRAINS. Espero que tenham gostado. E se você leu até aqui, parabéns! Você está empenhado de verdade.
Acredito que eu tenha conseguido passar de forma bastante didática alguns conceitos que podem ser confusos para quem está começando, mas que são conceitos fundamentais e indispensáveis para quem quer aprender Machine Learning.
Há ainda outras formas de medir a performance do modelo que eu gostaria de escrever sobre, como a Curva ROC e a Área Sob a Curva (AUC). Irei escrever sobre isso em breve, mas por enquanto vocês podem ficar com este link do Machine Learning Crash Course do Google Developers que é simplesmente sensacional.
Não deixe de conhecer um pouco mais sobre a nossa comunidade BRAINS – Brazilian AI Networks. Nosso objetivo é trazer, de forma colaborativa, conteúdo de qualidade sobre AI, ML e Dados em Português, para estudantes brasileiros.
Todos podem colaborar, de iniciantes a avançados. Para saber como, leia o nosso post BRAINS – Brazilian AI Networks.
Nos vemos em breve.



2 comentários