Como vocês já devem saber, uns dos temas principais aqui da nossa comunidade BRAINS, como o próprio nome já diz – Brazilian AI Networks – é Inteligência Artificial e Machine Learning. Anteriormente já fizemos uma introdução ao Machine Learning com o post Primeiramente, o que é Machine Learning? Logo depois, explicamos a teoria de Modelos de Regressão: Regressão Linear e apresentamos também uma abordagem Prática: Regressão Linear, com código em Python. Agora iremos falar sobre Regressão Logística.
Se você leu os posts citados acima (o que recomendamos bastante), você já tem uma base boa para se aprofundar um pouco mais nesse mundo. Mas ao mesmo tempo, é bem provável que se você leu, esteja se perguntando: “Espera ai! Mas aqui estamos falando de um problema de Regressão ou de Classificação?”
E se você se perguntou isso, a sua pergunta é totalmente pertinente! Afinal de contas, dividimos de forma bem clara os modelos de Regressão e os modelos de Classificação, e agora parece que misturamos os dois no mesmo título. Confuso? À primeira vista talvez, mas nos dê uma chance de explicar melhor.
Problemas e Algoritmos de Classificação
Nós já discutimos nos outros posts o que é o Aprendizado de Máquina Supervisionado, onde nós fornecemos para os modelos/algoritmos uma série de exemplos em forma de dados, com as suas respectivas saídas para cada exemplo. Quando temos um histórico de dados onde os exemplos são acompanhados das suas saídas, dizemos que são dados rotulados (a saída é chamada de rótulo, ou label).
Cada exemplo é uma entrada (input), representado por uma linha na base de dados por exemplo, e cada entrada tem uma série de características (features), e cada característica é normalmente representada por uma coluna na base de dados. Por convenção, costumamos chamar o conjunto de exemplos de entrada de \(X\), uma matriz de valores, e o conjunto de saídas ou rótulos de \(y\), um vetor de valores.
Como já sabemos, os algoritmos de Machine Learning irão percorrer os dados existentes, analisando todos os exemplos e seus respectivos rótulos, buscando padrões que possam ser aplicados em dados futuros. Podemos dizer que o algoritmo irá buscar uma função matemática que possa mapear uma entrada \(X\) à uma saída \(y\).
Quando estudamos os problemas de Regressão, vimos que são modelos que nos retornam valores exatos e contínuos. Como por exemplo o valor de um imóvel ou bem, o consumo de um carro, a receita de uma empresa, as vendas de um produto, etc.
Em problemas de Classificação, nossos modelos irão categorizar as entradas, ou seja, encaixar cada entrada em uma categoria, ou classe. Por exemplo, no caso do valor de um produto, ao invés de o modelo dizer que o produto deve custar R$17,50, ele vai dizer se o produto se encaixa na classe Barato ou na classe Caro. Ou até mesmo Barato, Médio ou Caro.
Aplicações de Modelos de Classificação
Um exemplo clássico de um algoritmo de Classificação é o Detector de Spam. Podemos ter outros, como aprovar ou não um empréstimo, produto bom ou com defeito… Qualquer tipo de problema que tenha como resposta uma entre várias classes, “sim” ou “não”, “aprovado” ou “reprovado”, “bom” ou “ruim”, 0 ou 1.
Para um detector de spam, a entrada \(X\) é o e-mail em si, mais precisamente todos as características deste e-mail: remetente, título, corpo do e-mail, se tem anexo ou não, destinatários, etc. A saída \(y\) vai ser se o e-mail é spam ou não é spam, ou seja, vamos classificar o e-mail nestas duas classes.
Havendo apenas duas classes, dizemos que é um problema de Classificação Binária. Três ou mais classes, torna-se uma Classificação Multiclasses. Vamos trabalhar hoje sobre a Classificação Binária.
Classificação Binária
Vamos voltar ao exemplo do modelo detector de spam.
O primeiro passo para este projeto é coletarmos dados, ou seja, exemplos de e-mails. Todos estes e-mails coletados, com suas respectivas características, devem ser rotulados. Para cada conjunto de características de um e-mail vamos ter um rótulo: não spam ou spam. Para simplificar iremos chamar não spam de 0 e spam de 1. Pois lembre-se, os modelos de Machine Learning trabalham com matemática. Palavras precisam ser convertidas em números para fazerem sentido, e isso se aplica às classes também.
Esse conjunto de dados rotulados, ou características com saídas de 0 ou 1, será nossa base de treino.

O que nosso modelo vai fazer é varrer a base de treino em busca de padrões. Ele vai passar a entender que determinadas características levam um e-mail a ser classificado como spam ou não. Com isso, após treinamento, ele deve conseguir classificar novos e-mails de forma eficiente.
A performance desse modelo vai depender principalmente da qualidade da nossa base de treino e do algoritmo escolhido. E por falar em algoritmo, vamos conversar sobre alguns.
Por que não Regressão Linear?
Podemos ver pelo título do post que vamos falar de Regressão Logística, que nada mais é do que uma extensão da Regressão Linear que nós já conversamos por aqui. Nós vamos entender o porquê de precisarmos da Regressão Logística. Mas antes, vamos entender o porquê de não usarmos Regressão Linear para problemas de classificação.
Iremos seguir com o exemplo de classificação de e-mails. Vamos supor que uma das características que nosso modelo rastreia é a quantidade de palavras-chave no corpo do e-mail. Essas “palavras-chave” são palavras comumente usadas em spams, como “promoção”, “sorteado”, “premiado”, etc.
É claro que nem todo e-mail que tem uma dessas palavras é automaticamente um spam. Sem dúvidas podemos ter e-mails com essas palavras que não são. Portanto, não é apenas a presença ou não destas palavras que faz o nosso modelo definir se é spam ou não, mas isso tem o seu peso. Então iremos analisar quantas destas palavras o e-mail possui para ajudar a classificá-lo como spam ou não.

Podemos verificar na tabela acima essa característica de cada e-mail e seu rótulo. Lembrando que cada linha da base de dados é um exemplo e cada coluna uma característica. Para fins de simplicidade, temos apenas uma característica e a nossa saída.
Visualizando os dados e modelos
Podemos plotar a distribuição dos dados acima em gráfico. Ficaria mais ou menos assim.
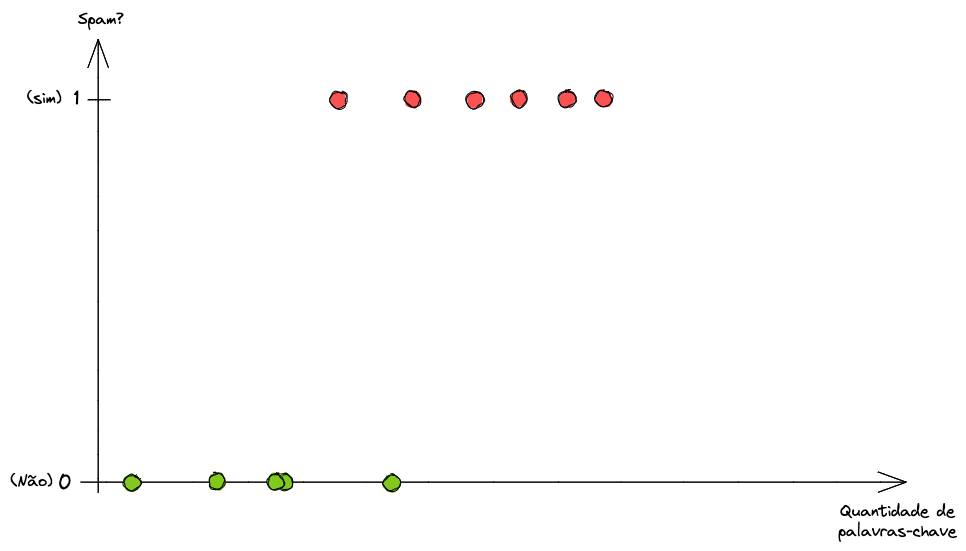
Note que no eixo Y temos as duas classes: 1 se o e-mail for spam e 0 se não for. Nós poderíamos tentar aplicar uma Regressão Linear para encontrar um padrão nos dados.
Possivelmente o modelo traria uma reta similar à esta.

De cara podemos ver que a reta não se encaixa muito bem aos dados. Poderíamos selecionar um limiar, um threshold, e dizer que qualquer valor acima desse limiar seria uma classe positiva e qualquer valor abaixo seria uma classe negativa. Vamos definir um limiar de \(0.5\).
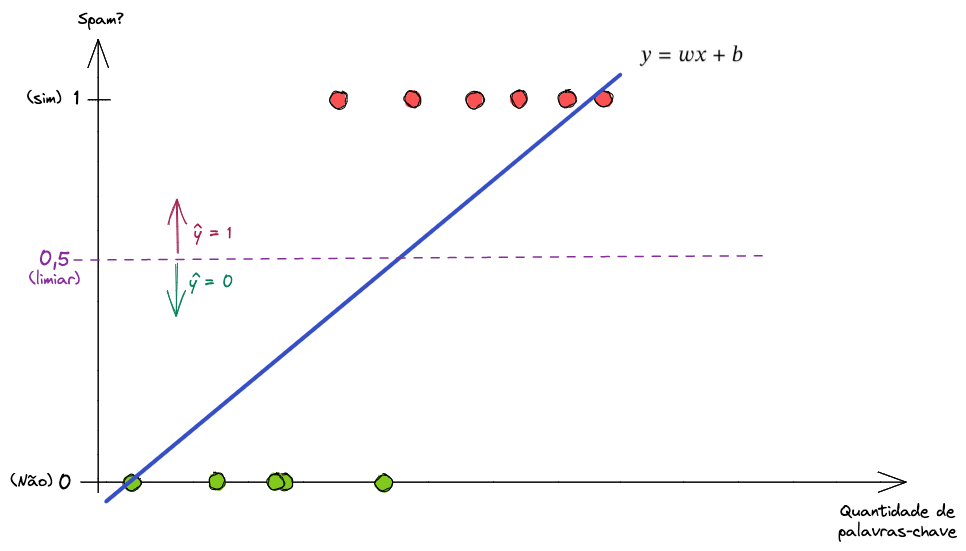
Note que há um ponto de intersecção entre a reta e o limiar. Isso quer dizer que tudo à esquerda dessa intersecção é exemplo negativo (não spam, ou 0) e tudo à direita é exemplo positivo (spam, ou 1).
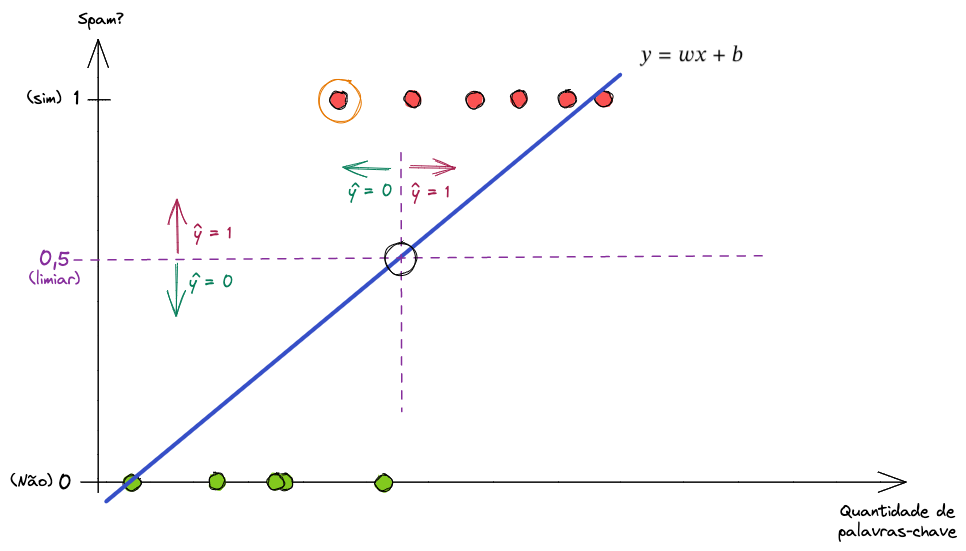
Nesse caso (simplificado), teríamos um erro ali. O modelo se sairia bem, né?
Poderia funcionar, mas isso ainda traz alguns problemas. Primeiro que o cálculo de perda da Regressão Linear não se aplicaria adequadamente. Segundo, esta reta pode assumir valores no eixo Y maiores que 1 e menores que 0. E nós não queremos isso. Lembre-se que uma classificação binária deve ter o seu valor de saída entre 0 e 1.
Adicionando novos exemplos
Além disso, vamos ver o que acontece ao adicionarmos mais um exemplo à esta nossa base de treino. Um bem à direita no eixo X.
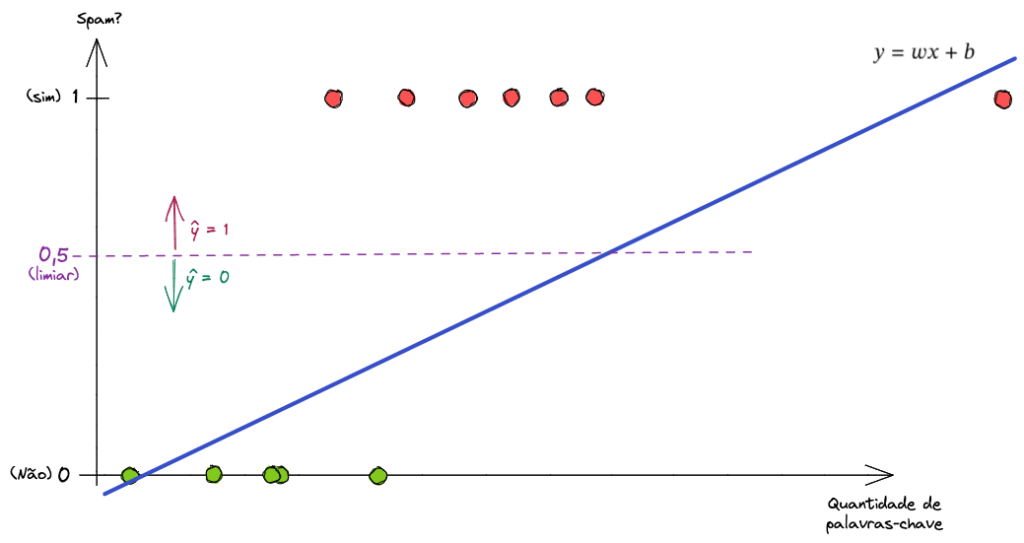
Note que para se ajustar à entrada do novo exemplo a Regressão Linear altera a sua fórmula matemática e muda a reta. Porém, agora o ponto de intersecção também é alterado, o que leva o modelo a cometer erros grotescos.
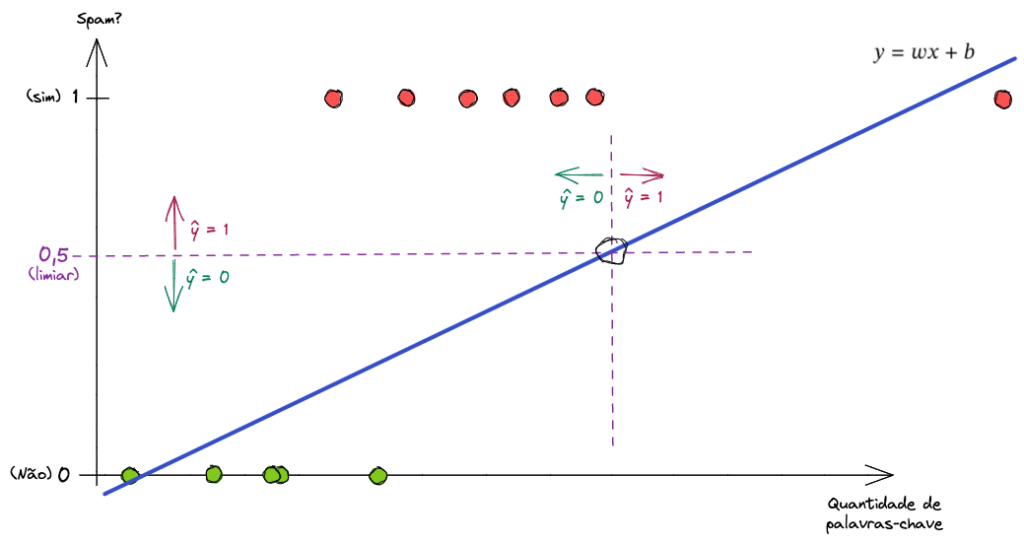
Agora este modelo se torna inútil para nós.
Por que Regressão Logística?
A Regressão Logística é, como falamos, uma extensão da Regressão Linear que consegue “espremer” os seus resultados para serem entre 0 e 1. E ela consegue isso fazendo uso de uma Função Logística sobre uma função linear.
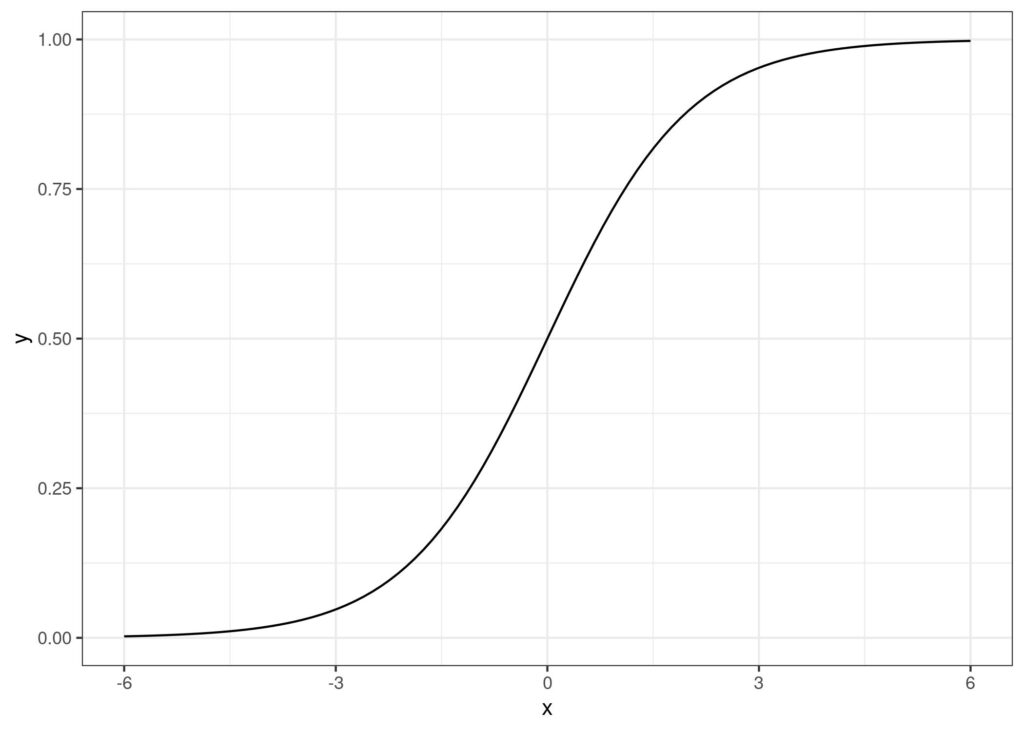
Uma Função Logística, que é uma Função Sigmoide, é muito característica por ter o seu formato em “S”. Novamente, note que não importa o valor do eixo X, o valor no eixo Y vai ser sempre entre 0 e 1, para x=0 vamos ter y=0.5.
A transformação de uma função linear em uma Regressão Logística é de certa forma fácil de entender. Vamos ver um pouco da sua teoria.
Teoria da Regressão Logística
Lembre-se que para uma Regressão Linear nós temos a função linear abaixo.
\[ \hat{y_{}}= wx + b \]
O que nós vamos fazer é aplicar uma função \(g()\) sobre a fórmula linear. Uma função não-linear, a Função Logística.
\[ \hat{y_{}}= g(wx + b) \]
A Função Logística irá calcular o “Logaritmo das Probabilidades” (Log of Odds), onde a probabilidade em questão é a de se ter um resultado positivo ( \(y\) ) dividido pela probabilidade de se ter um resultado negativo ( \(1 – y\) ), que é a “Relação das Probabilidades” (Odds Ratio).
\[ \frac{y}{1 – y} \to (y : 1 – y) \]
A Relação das Probabilidades é a probabilidade de positivo ( 1 ) dividido pela probabilidade de negativo ( 0 ). E o logaritmo disto é linear.
Disto isto, podemos encontrar a equação final da Função Logística.
\[ \log \left( \frac{\hat{y_{}}}{1 – \hat{y_{}}}\right) = wx + b \longrightarrow \hat{y_{}}= \frac{1}{1 + e^{-(wx + b)}} \]
Viram ali o \(wx + b\) da Regressão Linear? Para transformarmos na Regressão Logística, pegamos a função linear e encaixamos no denominador. A equação é \(1\) dividido por \(1\) mais \(e\) elevado a menos a função linear ( \(wx + b\) ).
Número \(e\) O número de Euler, denotado por \(e\), é uma constante matemática importante que tem muitas aplicações em diversas áreas da matemática, ciência da computação e outras ciências. Ele é a base do logaritmo natural.
Em Python podemos expressar o número \(e\) elevado a alguma coisa usando o códigonp.exp().
Sabemos agora como “espremer” uma Regressão Linear em uma Regressão Logística, para termos saídas entre 0 e 1, onde cada valor de saída representa uma probabilidade de tal entrada ser da classe positiva ( 1 ).
Deixaremos aqui a fórmula novamente.
\[ \hat{ y_{} } = \frac{1}{1 + e^{-(wx + b)}} \]
Aplicando a fórmula da Regressão Logística
Para entendermos como matematicamente a fórmula consegue manter os números entre zero e um, vamos testar com alguns valores. Iremos chamar o resultado intermediário da Regressão Linear (antes da Função Logística) de \(z\). Logo, podemos dizer que \(z = wx + b\).
\[ \hat{y_{}} = \frac{1}{1 + e^{-(z)}} \]
Suponhamos que o valor de \(z\) seja um número grande, como \(100\) por exemplo.
\[ z = 100 \]
\[ \hat{y_{}} = \frac{1}{1 + e^{-(100)}} \]
Sabemos que independente do valor de \(e\), este valor elevado a \(-100\) vai ser um número muito, muito pequeno. Podemos dizer que esse número pode ser arredondado para \(0\).
Ao desenvolvermos a fórmula teremos:
\[ \hat{y_{}} = \frac{1}{1 + e^{-(100)}} \longrightarrow \frac{1}{1 + 0} \]
\[ \hat{y_{}} = \frac{1}{1} = 1 \]
O valor final não seria exatamente \(1\), mas bem próximo disso.
Em contrapartida, quando temos um valor muito pequeno de \(z\), ou um valor negativo grande, como \(z = -100\), a fórmula irá agir de forma oposta.
Lembre-se que menos com menos dá mais. Então, \(e\) elevado a \(+100\) vai ser um número muito, muito grande. Desta forma, a fórmula fica sendo \(1\) sobre \(1\) mais um número enorme.
\[ \hat{y_{}} = \frac{1}{1 + e^{-(100)}} \longrightarrow \frac{1}{1 + (enorme)} \]
\[ \hat{y_{}} = \frac{1}{(enorme)} \approx 0 \]
Sabemos que \(1\) dividido por um número enorme vai ser muito próximo de \(0\).
Não é linda a forma como a matemática consegue fazer isso?
Voltando ao nosso modelo
De volta ao nosso algoritmo para detectar spam. Desta vez, vamos tentar encontrar uma Regressão Logística que se adeque bem aos dados. E vamos visualizá-la.

Faz bem mais sentido, certo? E o que aconteceria no caso de termos mais um exemplo bem à direita?
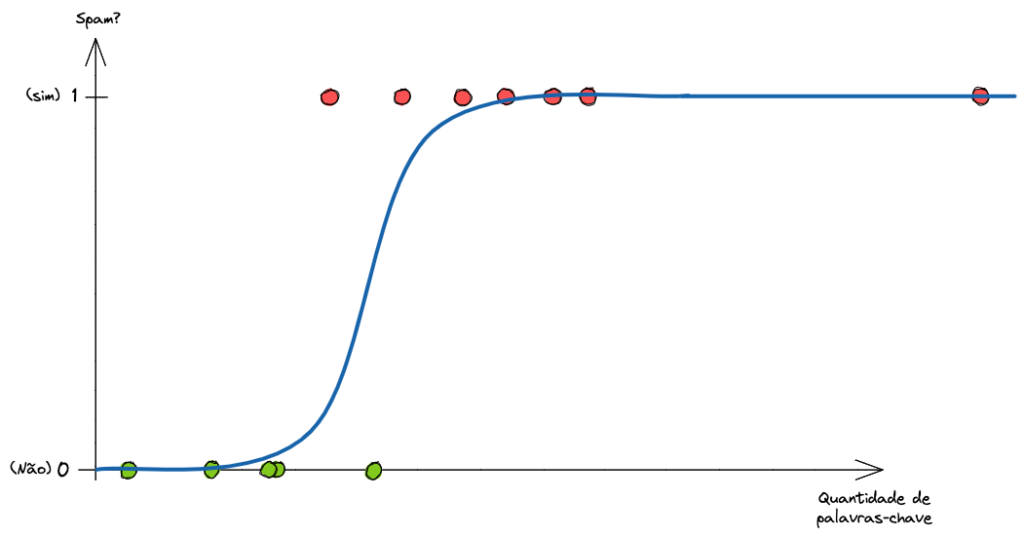
Isso não gera nenhum impacto negativo no nosso modelo. Perfeito!
Interpretando a Regressão Logística
Uma forma interessante de interpretar o resultado de uma Regressão Logística é que a sua saída é “a probabilidade de que a classe \(y\) vai ser igual a \(1\) dado uma certa entrada \(x\)“.
Desta forma, caso um determinado exemplo tenha um número \(x\) de palavras-chave e o nosso modelo nos dê de saída o valor previsto \(\hat{y_{}}\) de \(0.7\), podemos interpretar que este exemplo tem 70% de probabilidade de ser spam.
Novamente, podemos definir um limiar (threshold). Com este limiar, diremos que consideraremos como spam apenas entradas que tenham tantos porcento de probabilidade de ser spam.
Assim podemos ser conservadores e definir que iremos classificar como spam apenas quando tivermos 90% de probabilidade de que seja, para evitar termos e-mails importantes indo para a caixa de spam. Em contrapartida, podemos ser mais agressivos, e definir que 30% de probabilidade já é suficiente para não vermos o e-mail na nossa caixa de entrada.
O limiar padrão das bibliotecas de Regressão Logística é de \(0.5\). E a mesma lógica anterior se aplica para agora.
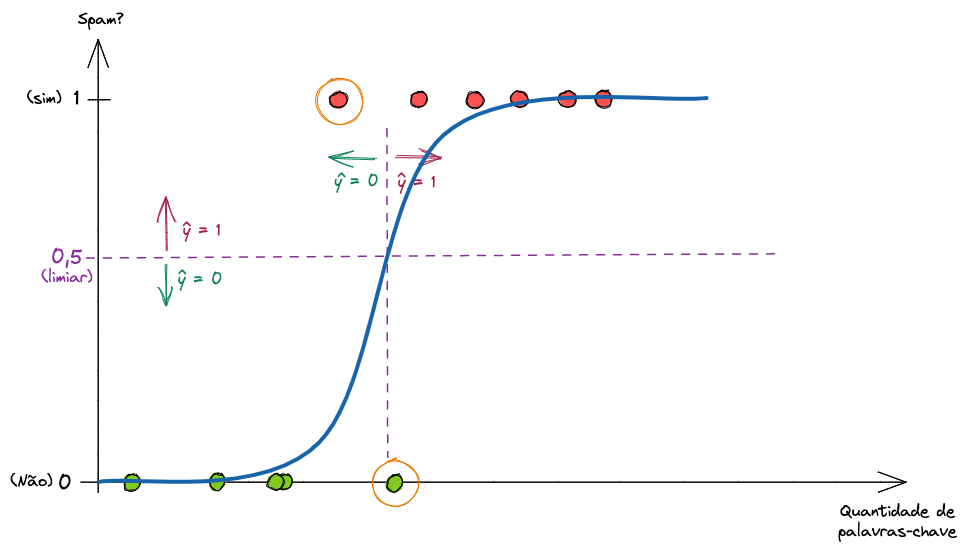
Note que nós temos dois erros (simplificando, novamente, em nome da didática). Porém se ajustarmos o nosso limiar, podemos ter uma quantidade de acertos maior (ou menor).

Ao trazermos o limiar para \(0.7\) conseguimos uma performance melhor do modelo, pois ele erra menos. Saber encontrar qual o limiar ideal faz parte do trabalho de um Cientista de Dados.
Em resumo, qualquer valor no eixo X irá retornar um valor no eixo Y que será entre 0 e 1. Este valor pode ser visto como porcentagem da probabilidade de a classe ser positiva, ou 1. Teremos valores de saída de 0% a 100%.
Encontrando a melhor Sigmoide
Assim como a Regressão Linear pode ter infinitas retas, porém apenas uma reta ideal, na Regressão Logísticas podemos ter diversas sigmoides. Mas precisamos encontrar a melhor função.

Novamente, diferentes combinações dos parâmetros \(w\) e \(b\) a serem aprendidos, irão resultar em diferentes Funções Logísticas. Para sabermos qual é a melhor, precisamos saber qual erra menos. Mas como medimos esse erro?
Medindo o erro da Regressão Logística
Na Regressão Linear nós encontramos a menor reta minimizando a perda, ou a Soma dos Quadrados das Diferenças. Infelizmente isso não funcionará com a Regressão Logística.
Não estamos mais calculando uma função linear, mas sim uma função logística. Por ser uma função não-linear, quando começamos a elevar os valores ao quadrado as coisas ficam complicadas. Minimizar a perda não é mais tão fácil, se tornando um problema não convexo. O que significa que se tentarmos resolver assim, teremos múltiplas respostas “corretas” para o mesmo problema, e não saberemos qual é a melhor de fato.
Isto pode ser explicado melhor ao entender os conceitos do algoritmo Gradiente Descendente Estocástico. Possivelmente falaremos em breve sobre isso por aqui.
O importante é que precisamos medir este erro, e a forma que fazemos isso é medindo o Logaritmo da Perda (Log Loss), ou a Entropia Cruzada (Cross-Entropy).
Relembrando as notações para o cálculo de erro, \(y\) representa o valor real e \(\hat{y_{}}\) representa o valor de saída do modelo. Esperamos que \(\hat{y_{}}\) seja igual a \(y\), ou o mais próximo possível disto.
Para calcular o Logaritmo da Perda (Log Loss), usaremos as seguintes fórmulas.
\[ \text{Log Loss} = \left\{ \begin{array}{cl}
– \log{(1 – \hat{y_{}})} & \text{ se } y = 0 \\
– \log{(\hat{y_{}})} & \text{ se } y = 1
\end{array} \right. \]
Ou seja, calculamos a perda com \(– \log{(\hat{y_{}})}\) se o valor real daquele exemplo for \(1\) ou com \(– \log{(1 – \hat{y_{}})}\) se o valor real daquele exemplo for \(0\).
Mas espera aí. Como assim “se”? A gente coloca um if / else no algoritmo? Matematicamente não funciona tão bem assim… Mas vamos ver novamente como a matemática é linda.
Desenvolvendo a fórmula de perda
Nós podemos desenvolver essa condicional com a seguinte fórmula.
\[ \text{Log Loss} = -y \log{(\hat{y_{}})} \ – (1 – y) \log{(1 – \hat{y_{}})} \]
Se \(y = 0\) o primeiro termo será cancelado, pois vamos multiplicar \(\log{(\hat{y_{}})}\) por \(0\). Assim, a fórmula fica:
\[ \text{Log Loss} = \ – \log{(1 – \hat{y_{}})} \]
Em contrapartida, se \(y = 1\), o segundo termo será cancelado. Iremos multiplicar \(\log{(1 – \hat{y_{}})}\) por \((1 – 1)\), ou seja, por \(0\). Neste caso, a fórmula fica:
\[ \text{Log Loss} = \ – \log{(\hat{y_{}})} \]
Linda a matemática, né?
Conseguimos assim uma forma convexa de medir a perda. Isso quer dizer que vamos conseguir encontrar uma única função logística ideal que se adapta melhor aos dados.
Vantagens e Desvantagens da Regressão Logística
A Regressão Logística é um modelo de classificação que nos retorna probabilidades, o que é extremamente poderoso. Apesar de termos visto aqui a sua aplicação para um problema de Classificação Binária, ela pode ser facilmente estendida para a Regressão Logística Multinomial. É um modelo extremamente fácil e rápido de se treinar e de gerar novas classificações.
Esta função é também uma das formas mais básicas de uma Rede Neural, podendo representar um neuron de uma rede neural profunda (Deep Neural Network). Iremos falar mais sobre isso no futuro.
Por outro lado, a Regressão Logística assume que as variáveis são independentes, não lidando bem com características que são correlacionadas. A interpretação dos seus coeficientes (ou parâmetros) também é complexa.
Conclusão
Esse post de novo acabou ficando um pouco longo – confesso que estou com dificuldades de encurtá-los ainda mais sem perder conteúdo necessário. Porém esperamos que vocês estejam gostando do nosso material e da nossa comunidade. Torcemos também para que tenham se interessado no assunto e queiram buscar mais informações.
É importante ressaltar que para modelos de Classificação, precisamos de métricas e técnicas diferentes para avaliar a performance do nosso modelo. Para saber um pouco mais sobre isso, você pode ler o nosso texto Medidas de Performance: Modelos de Classificação.
Caso queira ir além e ver uma forma prática de se implementar a Regressão Logística em código Python, você pode visitar este post: Prática: Regressão Logística para Classificação.
Se estiver com alguma dúvida, pode entrar em contato com a gente! Teremos o maior prazer em responder todos. E se você quiser contribuir escrevendo para nossa comunidade, será muito bem-vindo também! Para saber mais como contribuir, independente de você ser iniciante ou avançado, leia o nosso post BRAINS – Brazilian AI Networks.
O objetivo da nossa comunidade é trazer conteúdo de qualidade em Português sobre IA, Machine Learning e Dados para estudantes brasileiros. 🇧🇷
Junte-se a nós!




6 comentários
Conheci agora e que bom saber que existem conteúdos nessa qualidade traduzidos também! Muito obrigado!
Que legal, Anderson! Muito obrigado pelo feedback! Nós temos conteúdo traduzido e conteúdo gerados por nós mesmos, brasileiros. Esse post foi um escrito por nós aqui mesmo! 🙂