Prática: Regressão Linear, com código em Python

Para complementar o nosso post teórico, Modelos de Regressão: Regressão Linear, iremos trazer um pouco de prática, desenvolvendo em Python uma Regressão Linear utilizando a biblioteca statsmodel.

Recomendamos fortemente a leitura do post citado acima para podermos contextualizar o que iremos desenvolver aqui. Então vamos lá, à prática! 🧑🏻‍💻

Caso deseje executar esse código de forma interativa, disponibilizamos o Notebook no Google Colab. Basta acessar o link para executar e editar o código como bem entender.

Objetivos

Nós iremos construir um Modelo de Regressão Linear para tentar prever o consumo de um carro (mpg, ou miles per gallon).

Note que – assim como muitos datasets públicos – a base de dados está em Inglês, tanto nos seus textos quanto nas suas unidades de medidas.

Descrição dos Dados

É sempre importante para o Cientista de Dados entender do que se trata a base de dados antes mesmo de iniciar o processo de modelagem.

Esta nossa base de dados (dataset) é composta por 9 variáveis, incluindo o nome do carro e outras características do automóvel, como potência, peso, origem da fabricação, etc.

Valores faltantes são marcados na base de dados como pontos de interrogação ( ? ).

Uma descrição detalhada das variáveis está disponível abaixo.

1. mpg: milhas por galão (medida de consumo dos EUA, como km/L), nossa variável alvo
2. cylinders: número de cilindros do motor
3. displacement: deslocamento do motor, em polegadas cúbicas
4. horsepower: potência do carro, em HP
5. weight: peso do carro, em libras
6. acceleration: tempo, em segundos, para acelerar de 0 a 60 mph (milhas por hora)
7. model year: ano de fabricação do carro
8. origin: região da origem do carro (1 – Americano / 2 – Europeu / 3 – Asiático)
9. car name: nome do carro

Bibliotecas para Regressão Linear

# Manuseio dos dados
import pandas as pd
import numpy as np

# Visualização
import matplotlib.pyplot as plt
import seaborn as sns

# Divisão da base de dados
from sklearn.model_selection import train_test_split

# Modelo de Regressão Linear
import statsmodels.api as sm

# Avaliação da performance do modelo
from sklearn.metrics import mean_absolute_error, mean_squared_error

Note que nós decidimos construir nosso modelo de Regressão Linear usando a biblioteca stasmodels, que traz diversas funções matemáticas e estatísticas de forma conveniente para nós.

Entretanto, seria perfeitamente possível utilizar outras bibliotecas, como a scikit-learn, por exemplo, para a construção do mesmo modelo.

Carregando e Explorando os Dados

# Local do dataset online
url_dataset = 'https://raw.githubusercontent.com/lopes-andre/datasets/main/auto-mpg.csv'

# Carrega os dados em um DataFrame
cdata = pd.read_csv(url_dataset)
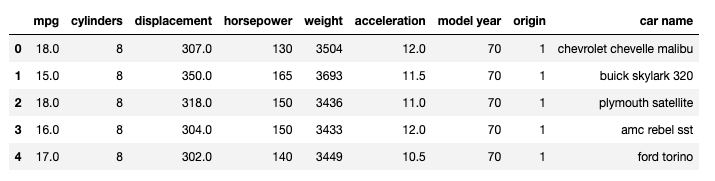
cdata.head()

Teremos como saída as cinco primeiras linhas do DataFrame Pandas.

Vamos verificar o shape dos dados, ou seja, as dimensões que nossa base de dados tem. Como se trata de uma base tabular, teremos apenas duas dimensões: linhas e colunas.

# Verifica o shape dos dados
print(f'Shape dos dados: {cdata.shape}\n')

print(f'Esta base de dados tem {cdata.shape[0]} linhas e {cdata.shape[1]} colunas.')

Saída:

Shape dos dados: (398, 9)

Esta base de dados tem 398 linhas e 9 colunas.

E com apenas uma linha de código, podemos ter todo o resumo estatístico dos dados.

# Resumo Estatístico dos dados
cdata.describe()

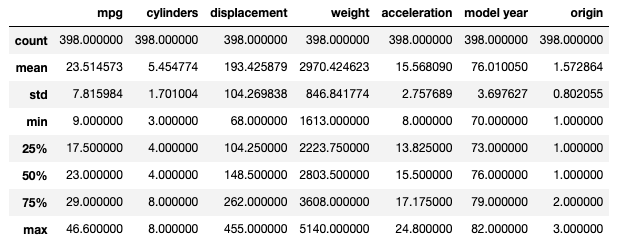
Observações

• Este método nos retorna as seguintes informações:
  • Contagem de entradas de cada coluna.
  • Média.
  • Desvio Padrão.
  • Valores mínimo e máximo de cada coluna.
  • Primeiro quartil, Mediana e terceiro quartil.
• Todas as entradas numéricas são retornadas.

Note que a coluna de potência do carro, horsepower, não apareceu como retorno.

Vamos tentar entender o ocorrido.

# Verifica os tipos das colunas e quantidade de entradas
cdata.info()

Observações

• Note que não temos dados nulos, todas as colunas estão com contagem de 398 non-null. Porém, lembre-se que o que é dado faltante está marcado com o ponto de interrogação ( ? ) e isso deve ser analisado.
• A maioria das colunas são de dados numéricos (Dtype do tipo int64 ou float64).
• As colunas horsepower e car name são colunas de strings (tipo object).

Nós iremos dropar (ou remover) a coluna com o nome do carro, já que isso é apenas um identificador e não agrega nenhum valor preditivo ao nosso modelo.

A coluna de potência deveria, em teoria, ser numérica também. Precisamos analisar e encontrar o porquê de ela estar como string.

# Dropa a coluna `car name`
cdata = cdata.drop('car name', axis=1)

Lidando com Valores Faltantes

Vamos analisar melhor para checar se não há valores nulos/faltantes na nossa base de dados, apesar de a contagem ter nos apresentado que todas as entradas estão como non-null.

Iremos verificar a coluna horsepower para ver o porquê de ela estar sendo tratada como string e não como numérica.

Para isto, criaremos um filtro para encontrar entradas que possam estar demarcadas com ? ao invés de um dígito.

# Cria um filtro com True onde a entrada é um dígito
# e False onde não é um dígito
hp_is_digit = cdata['horsepower'].str.isdigit()

# Imprime as entradas onde isdigit=False
cdata.loc[hp_is_digit == False]

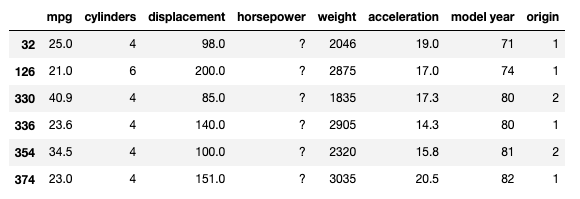
Observações

• Nós sabemos que ? marca valores faltantes na base de dados. E podemos ver que este ponto de interrogação foi encontrado algumas vezes na coluna de potência do motor ( horsepower ).
• Iremos substituir esses valores por np.NaN (marcador do NumPy que denota um valor não-numérico dentro de uma coluna numérica, NaN significa Not a Number).

Esta substituição irá nos permitir lidar com os valores faltantes de forma mais elegante.

# Substitui '?' por np.NaN
cdata = cdata.replace('?', np.nan)
cdata.loc[hp_is_digit == False]

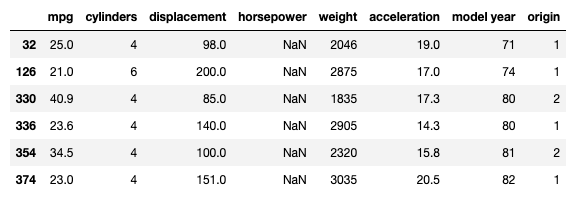
Agora que a coluna horsepower não tem mais strings, podemos convertê-la para o tipo float64 e tratá-la como uma coluna numérica.

# Converte a coluna `horsepower` do tipo objeto para o tipo float
cdata['horsepower'] = cdata['horsepower'].astype(float)
cdata.info()

Note que agora a coluna horsepower tem apenas 392 non-null na sua contagem, indicando 6 entradas faltantes.

Existem diversas formas de tratar valores faltantes. Nós podemos remover as entradas, substituir os valores faltantes com a Média ou Mediana das colunas, ou muitas outras abordagens.

Ao invés de dropar/remover essas linhas com valores faltantes, iremos substituir os valores faltantes com a sua Mediana.

# Verifica a mediana das colunas
cdata.median()

Podemos com apenas uma linha de código substituir os valores faltantes ( NaN ) pela mediana dos valores da coluna.

# Substitui os valores faltantes com a Mediana da coluna
cdata['horsepower'] = cdata['horsepower'].fillna(cdata['horsepower'].median())

Substituindo os valores da origem

Iremos substituir os valores da origem do carro por seus nomes reais, conforme descrito na introdução.

É necessário fazer isso pois quando temos números inteiros nós temos uma ordem explícita. 1 é menor que 2, que é menor que 3… Porém América não é menor que Europa, que por sua vez não pode ser comparada como menor ou maior que Ásia.

Logo, a coluna origin não é uma coluna de valores ordinais, e precisamos remover esta ordem presente nos seus dados.

Para isso, vamos trocar 1 por “america”, 2 por “europa” e 3 por “asia”.

# Cria dicionário para substituição
subs_dict = {
    1: 'america',
    2: 'europa',
    3: 'asia'
}

# Substitui no DataFrame
cdata['origin'] = cdata['origin'].replace(subs_dict)
cdata.head()

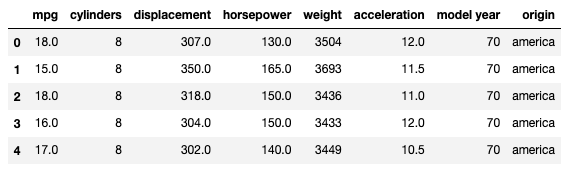
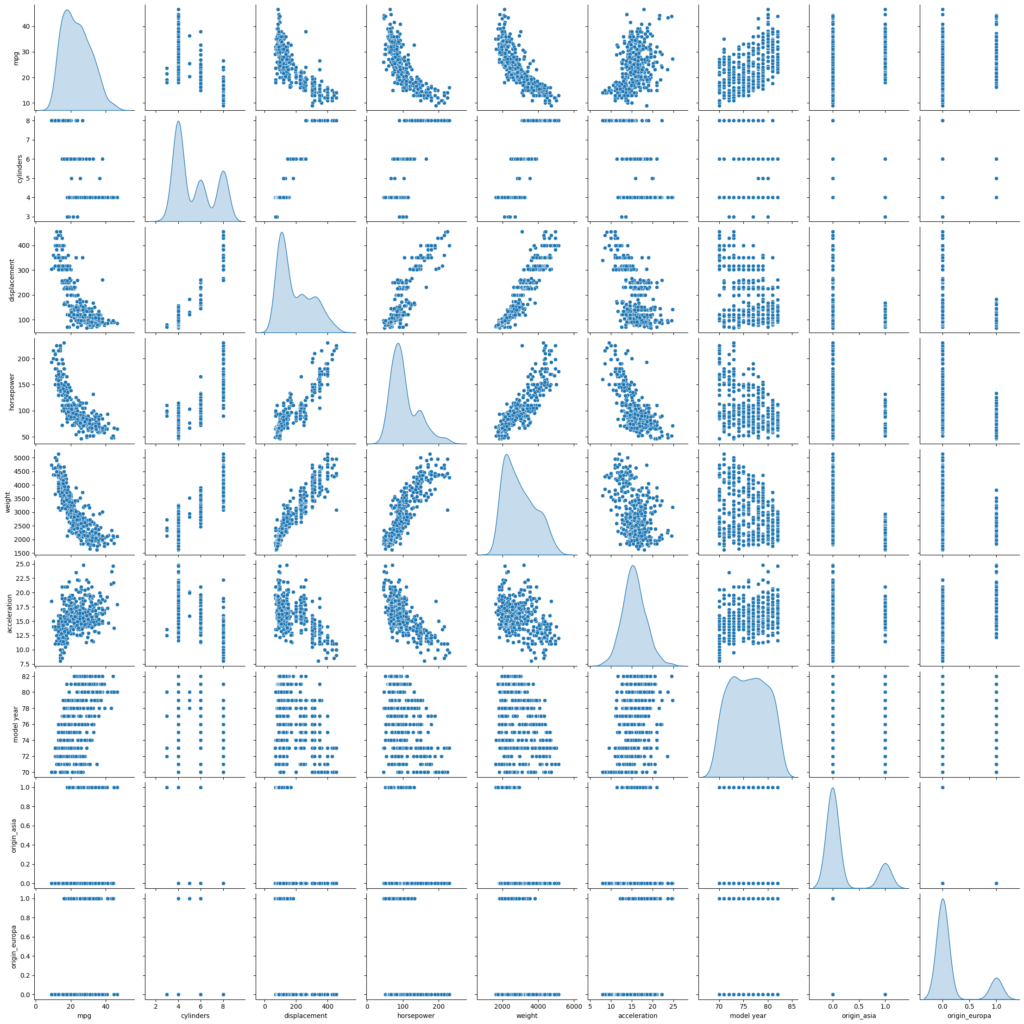
Análise de Dados Bivariada

A Análise de Dados Bivariada entre as diferentes variáveis pode ser feita usando o gráfico da Matriz de Dispersão (usando sns.pairplot() ).

A biblioteca Seaborn cria um dashboard refletindo as informações sobre as dimensões da nossa base de dados.

# Exibe a Matriz de Dispersão
sns.pairplot(cdata, diag_kind='kde')

Para simplificar, podemos exibir apenas a relação entre a nossa variável alvo com as outras.

# Exibe apenas a relação entre mpg e as outras variáveis
sns.pairplot(cdata, diag_kind='kde', y_vars=['mpg'])

Observações

• Observe que a relação entre mpg e as outras variáveis não é exatamente linear.
• Entretanto, os gráficos indicam que linearidade ainda assim capturaria um tanto de informação/padrão relevante e útil.
• Muitas premissas de uma Regressão Linear Clássica parecem ser violadas.

Criação de Variáveis Dummy

Valores como america não podem ser lidos em uma equação. Usar os valores 1, 2 e 3 para substituir america, europa e asia acabaria implicando na ordinalidade que comentamos. Não faz sentido falarmos que carros europeus estão exatamente no meio do caminho entre carros americanos e asiáticos. Nós não podemos impor esse tipo de comparação sem base.

Então nós aplicaremos uma técnica chamada OneHotEncoding, que irá criar 3 colunas simples de True ou False com o título equivalente a “Este carro é Americano?“, “Este carro é Europeu?” e “Este carro é Asiático?“.

Estas 3 colunas vão ser usadas como variáveis independentes sem precisarmos impor nenhuma ordem entre os três continentes.

Note que cada observação, cada exemplo de carro, só vai poder ser verdadeiro em uma dessas três novas colunas, dado que um carro não pode ser americano e europeu ao mesmo tempo.

Logo, para entradas onde a origem é america, apenas a coluna da América terá valor de True e as outras duas serão False.

Para maior eficiência do código, e para evitar Dependência Linear, podemos remover uma das três colunas e caso as duas colunas que ficarem sejam False, saberemos então que este exemplo diz respeito à terceira coluna implícita.

# Cria o OneHotEncoding
cdata = pd.get_dummies(cdata, columns=['origin'], drop_first=True)
cdata.head()

Neste ponto, finalizamos a preparação dos dados

Divisão dos Dados para Regressão Linear

Iremos separar as características do carro, as variáveis independentes, da nossa variável alvo, ou variável dependente.

Lembre-se que chamamos de X o conjunto de características do carro (features) e chamamos de y a nossa resposta de interesse, nossa variável alvo a ser descoberta (target).

Será necessário também adicionar uma constante de 1.0 à matriz X de características para que o algoritmo possa realizar seus cálculos de forma precisa e eficiente.

# Variáveis independentes (características)
X = cdata.drop(['mpg'], axis=1)

# Variável dependente (alvo)
y = cdata['mpg']

# Adiciona a constante
X = sm.add_constant(X)

Divisão dos dados em Base de Treino e Base de Teste

É muito importante dividirmos a base de dados entre Treino e Teste para simular como o modelo vai se comportar em produção, evitar Overfitting e termos métricas de performance precisas.

Iremos fazer a divisão dos dados na proporção de \(70:30\), ou seja, 70% dos dados para Treino e 30% dos dados para Teste.

# Divisão dos dados em Treino e Teste
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

Treino do Modelo de Regressão Linear

O treino do modelo é extremamente simples – a dificuldade está na preparação correta dos dados.

Nós iremos usar o algoritmo de Ordinary Least Squares para encontrar os parâmetros (ou coeficientes) da nossa Regressão.

Para isso iremos instanciar um objeto sm.OLS() e fazermos com que ele se adapte aos nossos dados, ou seja, que ele treine sobre os dados, com o método .fit().

# Instancia e treina o modelo
olsmod = sm.OLS(y_train, X_train)
olsres = olsmod.fit()

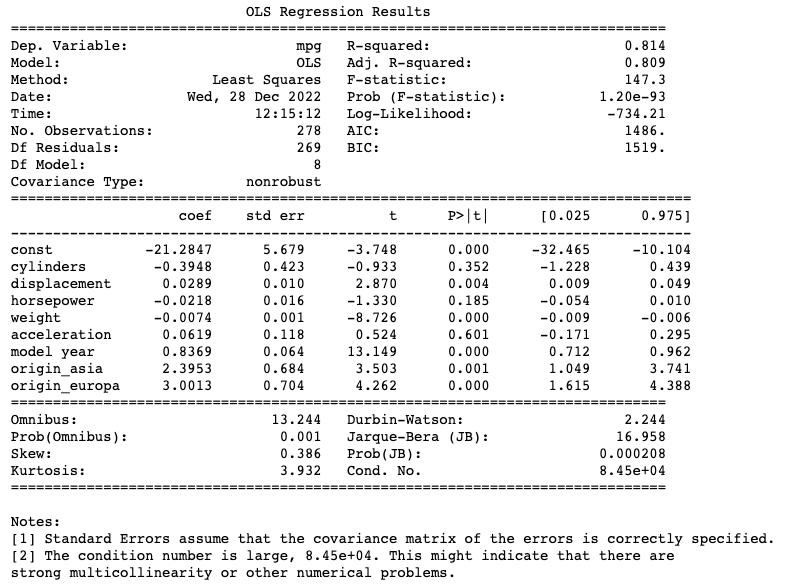
Com apenas mais uma linha de código podemos ter todo o resumo da nossa regressão, que nos traz informações muito importantes como o coeficiente (𝑤, ou weights) de cada característica, a medida de R² da regressão, e muito mais.

# Imprime o resumo da regressão
print(olsres.summary())

Avaliação do Modelo de Regressão Linear

Agora iremos verificar a medida de MAE e MSE, tanto na base de treino quanto na base de testes.

# Imprime as métricas de MAE
print(f'Métrica MAE na base de treino: {mean_absolute_error(y_train, olsres.predict(X_train))}')
print(f'Métrica MAE na base de teste: {mean_absolute_error(y_test, olsres.predict(X_test))}')

Saída:

Métrica MAE na base de treino: 2.653320760010246
Métrica MAE na base de teste: 2.354281207220391

# Imprime as métricas de MSE
print(f'Métrica MSE na base de treino: {mean_squared_error(y_train, olsres.predict(X_train))}')
print(f'Métrica MSE na base de teste: {mean_squared_error(y_test, olsres.predict(X_test))}')

Saída:

Métrica MSE na base de treino: 11.521429009864104
Métrica MSE na base de teste: 9.16097967896145

Conclusão sobre a Regressão Linear

O modelo foi treinado com sucesso. A métrica de R² nos mostra que o modelo consegue explicar 81,4% da variância dos dados e as métricas de MSE e MAE nos mostram que o modelo tem uma performance aceitável, dentro das suas limitações.

Assim concluímos este rápido laboratório de como treinar uma Regressão Linear.

Caso tenha ficado com alguma dúvida, entre em contato conosco pelos comentários.

Colabore com a nossa comunidade trazendo conteúdo de qualidade em Português, seja conteúdo próprio ou traduzido. Iremos ficar muito felizes de receber material de vocês.

Para conhecer mais sobre nós e saber como colaborar, visite o post abaixo.

• BRAINS – Brazilian AI Networks 🧠

É sempre um prazer estar com vocês por aqui!

#NoBrains #NoGains 🧠