Prática: Regressão Logística para Classificação

Recentemente publicamos dois posts muito importantes como introdução aos modelos de Aprendizado Supervisionado de Classificação e sobre o algoritmo de Regressão Logística.

O primeiro, Modelos de Classificação: Regressão Logística, nos apresenta a teoria dos modelos de classificação e nos traz este novo algoritmo. Não se deixe enganar, apesar de ter “Regressão” no nome, trata-se de um modelo de classificação. O segundo, Medidas de Performance: Modelos de Classificação, é extremamente importante para entender como avaliamos estes modelos.

Agora nós iremos colocar as mãos na massa no teclado! Vamos desenvolver um modelo de classificação em Python utilizando o algoritmo de Regressão Logística.

Se preferir, é possível executar esse código como Notebook no Google Colab. Basta acessar o link para executar e editar o código como preferir.

Objetivos

Diabetes é uma das doenças mais frequentes do mundo de hoje e o número de pacientes diabéticos vem crescendo nos últimos anos. A principal causa raiz da diabetes continua desconhecida, mas muitos cientistas acreditam que ambos, fatores genéticos e de estilo de vida, são quesitos importantes no desenvolvimento da doença.

Dada a seriedade e complexidade da doença, vamos construir um modelo de Classificação Binária para tentar prever se uma pessoa tem probabilidade de desenvolver diabetes ou não.

Descrição dos Dados

Vamos trabalhar sobre um dataset originalmente do National Institute of Diabetes and Digestive and Kidney Diseases, hoje disponível no Kaggle, chamado Pima Indians Diabetes Database.

A base de dados é constituída apenas por mulheres com mais de 21 anos e descendentes do povo Pima da Índia. O dataset possui 9 colunas.

Sabemos que entender os dados é passo fundamental do trabalho de um Cientista de Dados. Portanto, vamos analisar uma descrição detalhada das variáveis disponíveis.

1. Class: variável de classe, ou variável alvo (0: a pessoa não é diabética / 1: a pessoa é diabética).
2. Pregnancies: número de gravidezes.
3. Glucose: concentração de glicose plasmática durante 2 horas em um teste oral de tolerância à glicose.
4. BloodPressure: pressão sanguínea diastólica (mm Hg).
5. SkinThickness: espessura da dobra cutânea do tríceps (mm).
6. Insulin: nível de insulina no sangue (mu U/ml).
7. BMI: IMC, Índice de Massa Corporal (peso em kg/(altura em m)²).
8. Pedigree: função hereditária – uma função que classifica a probabilidade de diabetes baseada no histórico familiar exclusivamente.
9. Age: idade em anos.

Bibliotecas para Regressão Logística

# Manuseio dos dados
import numpy as np
import pandas as pd

# Visualização
import matplotlib.pyplot as plt
import seaborn as sns

# Divisão da base de dados
from sklearn.model_selection import train_test_split

# API para modelo de Regressão Logística
import statsmodels.api as sm

# Avaliação da performance do modelo
from sklearn import metrics
from sklearn.metrics import (accuracy_score, 
                             confusion_matrix, 
                             recall_score, 
                             precision_score)

Nós iremos construir nosso modelo de Regressão Logística usando a biblioteca statsmodels, que traz diversas funções matemáticas e estatísticas de forma conveniente para nós.

Entretanto, seria perfeitamente possível utilizar outras bibliotecas, como a scikit-learn, por exemplo, para a construção do mesmo modelo.

Carregando e Explorando os Dados

# Local do dataset online
url_dataset = 'https://raw.githubusercontent.com/lopes-andre/datasets/main/pima-indians-diabetes.csv'

# Carrega os dados em um DataFrame
data = pd.read_csv(url_dataset)
data.head()

Os dados são carregados numa estrutura chamada Pandas DataFrame. Temos como saída as cinco primeiras entradas da base de dados.

Vamos verificar o shape dos dados, ou seja, as dimensões que nossa base de dados tem. Como se trata de uma base tabular simples, teremos apenas duas dimensões: linhas e colunas.

# Verifica o shape dos dados
print(f'Shape dos dados: {data.shape}\n')

print(f'Esta base de dados tem {data.shape[0]} linhas e {data.shape[1]} colunas.')

Temos como saída:

Shape dos dados: (768, 9)

Esta base de dados tem 768 linhas e 9 colunas.

E com apenas uma linha de código, podemos ter todo o resumo estatístico dos dados.

# Resumo Estatístico dos dados
data.describe()

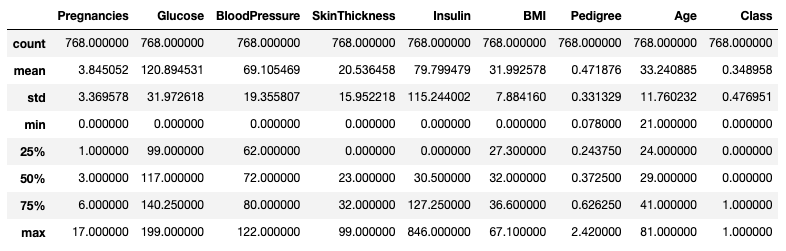
Observações

• Nós podemos com apenas uma linha de código ver todo o resumo estatístico dos dados.
• Este método nos retorna as seguintes informações:
  • Contagem de entradas de cada coluna.
  • Média.
  • Desvio Padrão.
  • Valores mínimo e máximo de cada coluna.
  • Primeiro quartil, Mediana e terceiro quartil.
• Todas as entradas numéricas são retornadas. Neste caso, todas as colunas.

Com mais apenas uma linha podemos verificar os tipos de dados de cada coluna.

# Verifica os tipos das colunas e quantidade de entradas
data.info()

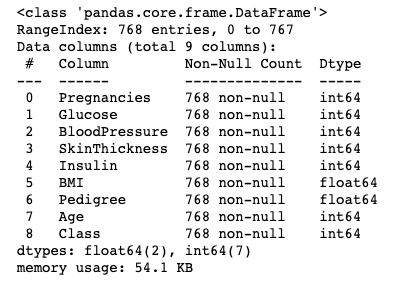
Note que aparentemente não temos nenhum dado nulo ou faltante. Temos 768 linhas na base e todas as colunas possuem 768 dados não nulos.

Vamos executar um código especificamente para verificar isso.

# Verifica dados nulos/faltantes
data.isnull().values.any()

E temos como saída:

False

Observações

• Note que de fato não temos dados nulos. Todas as colunas estão com contagem de 768 non-null e temos 768 linhas na base. Usamos também o método .isnull() seguido por .any() para verificar a presença de algum dado nulo. Esta cadeia de métodos nos retorna apenas False, ou seja, sem dados nulos.
• Todas as colunas são de dados numéricos (Dtype do tipo int64 ou float64). Não vamos precisar tratar colunas categóricas com técnicas como OneHotEncoding.

Análise de Dados Univariada

A Análise de Dados Univariada irá focar na distribuição das variáveis de forma individual. Iremos usar Histogramas ( data.hist() ) para analisar a distribuição dos dados.

Iremos usar o próprio Pandas para plotar todas as distribuições de uma só vez.

# Plota Histogramas para toda a base de dados
sns.set_style('darkgrid')
data.hist(figsize=(15,10))
plt.show()

E temos como resultado os seguintes gráficos.

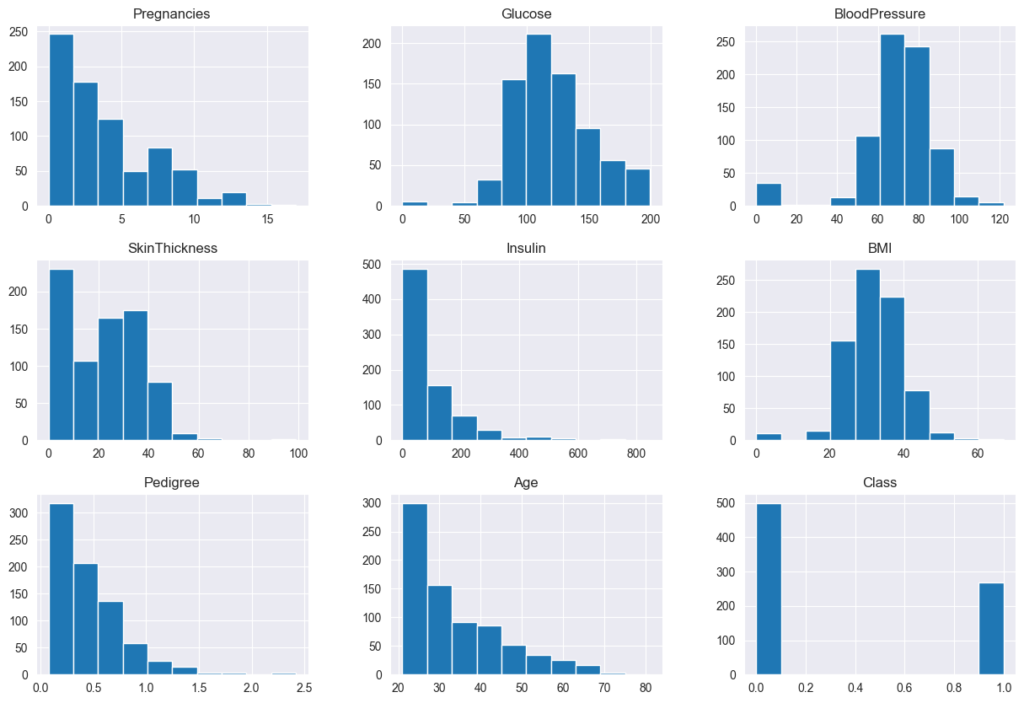
Observações

• Reparem que as colunas Glucose, BloodPressure, SkinThickness, Insulin e BMI têm observações com valores de 0, o que não é possível. Essas entradas representam erros nos dados e nós precisamos corrigi-los.
• Iremos substituir os valores de 0 em todas as colunas, exceto nas de Pregnancies e Class, por np.nan, um marcador do NumPy que denota um valor não-numérico dentro de uma coluna numérica (NaN significa Not a Number).

Esta substituição irá nos permitir lidar com os valores faltantes de forma mais elegante.

# Colunas para converter 0 em NaN
cols = ['Glucose', 'BloodPressure', 'SkinThickness', 
        'Insulin', 'BMI', 'Pedigree']

# Substitui 0 em NaN
data[cols] = data[cols].replace(0, np.nan)

Após substituição, analisaremos os dados nulos/faltantes novamente.

# Verifica valores nulos novamente
data.isnull().sum()

Lidando com Valores Faltantes

Após substituirmos os valores de 0 em colunas onde zero é impossível por np.nan, descobrimos que na verdade temos sim valores faltantes que precisam ser imputados.

Existem diversas formas de tratar valores faltantes. Nós podemos remover as entradas, substituir os valores faltantes com a Média ou Mediana das colunas, ou muitas outras abordagens.

Ao invés de dropar/remover essas linhas com valores faltantes, iremos substituir os valores faltantes com a média da coluna.

# Imputando os valores nulos com a média
data[cols] = data[cols].fillna(data[cols].mean())

Após o tratamento dos dados faltantes, podemos verificar novamente se ainda temos presença de dados nulos na nossa base.

# Verifica valores nulos novamente
data.isnull().sum()

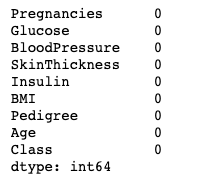
Não temos mais dados nulos/faltantes.

Podemos voltar e fazer uma análise gráfica mais coerente.

Análise de Dados Univariada

Vamos novamente analisar a distribuição dos dados.

# Plota Histogramas para toda a base de dados
sns.set_style('darkgrid')
data.hist(figsize=(15,10))
plt.show()

Análise de Dados Bivariada

A Análise de Dados Bivariada entre as diferentes variáveis pode ser feita usando o gráfico de Mapa de Calor (usando sns.heatmap() ) sobre a tabela de correlação dos dados ( data.corr() ).

Nesta representação gráfica conseguimos observar a correlação entre as diferentes variáveis da nossa base de dados. Note que os valores de correlação variam de \(−1\) a \(1\), onde \(−1\) representa uma correlação máxima negativa (ou seja, quando uma variável aumenta a outra diminui) e \(1\) representa uma correlação máxima positiva (quando uma variável aumenta, a outra também aumenta).

Uma correlação de \(0\) indica que não há correlação nenhuma entre as duas variáveis.

A biblioteca Seaborn cria um Mapa de Calor (Heat Map) refletindo estas correlações.

# Mapa de Calor para Correlação
plt.figure(figsize=(15,7))
sns.heatmap(data.corr(), annot=True, vmin=-1, vmax=1)
plt.show()

Observações

• Não temos nenhum caso de correlação significativamente alta, tanto positiva quanto negativa, entre as variáveis.
• A escala de cores nos ajuda a identificar os casos de alta correlação.

Note que a correlação entre uma variável e ela mesma é sempre \(1\). Portanto, temos esta diagonal no mapa de calor com \(1\) e uma cor mais clara.

Distribuição da Variável Alvo

Por ser um problema de Classificação Binária, é importante analisarmos a distribuição das duas classes da nossa variável alvo.

Conversamos brevemente sobre classes desbalanceadas e os problemas que podem trazer para o modelo no post Medidas de Performance: Modelos de Classificação. Vamos ver se temos este desbalanceio aqui.

# Contagem dos valores em cada classe
data['Class'].value_counts()

# Porcentagem dos valores em cada classe
data['Class'].value_counts(normalize=True)

Observações

• A classe 0 (não diabéticos) tem 500 exemplos. Isto representa 65% da nossa base de dados.
• A classe 1 (diabéticos) tem 268 exemplos. Em torno de 35% dos dados.

Finalizamos a preparação dos dados.

Divisão dos Dados para Regressão Logística

Iremos agora separar as características de cada paciente, as variáveis independentes, da nossa variável alvo, ou variável dependente.

Lembre-se que chamamos de X o conjunto de características (features) e chamamos de y a nossa resposta de interesse, nossa variável alvo a ser descoberta (target).

Será necessário também adicionar uma constante de 1.0 à matriz X de características para que o algoritmo possa realizar seus cálculos de forma precisa e eficiente.

# Variáveis independentes (características)
X = data.drop(['Class'], axis=1)

# Variável dependente (alvo)
y = data['Class']

# Adiciona a constante
X = sm.add_constant(X)

Precisamos agora dividir a nossa base de dados entre Treino e Teste. Já discutimos a importância desta divisão, onde separamos uma parte dos dados (70% neste caso) para realizarmos o treino do modelo e uma outra parte (30%) para testarmos e vermos se o modelo de fato aprendeu, ou se apenas “decorou” respostas e se “ajustou demais” ao problema (Overfitting).

Como temos um certo desbalanceio na nossa variável alvo, é interessante mantermos as mesmas proporções de classes positivas e negativas tanto na base de treino quanto na de teste. A divisão é aleatória, e não queremos perder esta proporção.

Para isso, iremos fazer uso do argumento stratify=y da função train_test_split() disponível na biblioteca Scikit-learn. Este argumento irá manter as devidas proporções das classes de y para treino e teste.

# Divisão dos dados em Treino e Teste
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                                   test_size=0.30,
                                                   random_state=1,
                                                   stratify=y) # mantém as proporções das classes

Treino do Modelo de Regressão Logística

O treino do modelo é extremamente simples – a dificuldade está na preparação correta dos dados.

Nós iremos usar o algoritmo de Logit para encontrar os parâmetros (ou coeficientes) que se adequam melhor à nossa Regressão.

Para isso iremos instanciar um objeto sm.Logit() e fazermos com que ele se adapte aos nossos dados, ou seja, que ele treine sobre os dados, com o método .fit().

# Instancia e treina o modelo
logit = sm.Logit(y_train, X_train.astype(float))
lg = logit.fit()

Com apenas mais uma linha de código podemos ter todo o resumo da nossa Regressão Logística, que nos traz informações muito importantes como o coeficiente (𝑤, ou weights) de cada característica, entre outras.

# Imprime o resumo da Regressão Logística
print(lg.summary())

Observações

• Os coeficientes da Regressão Logística são em termos logarítmicos, em Log of Odds ( \(\log(odds)\) ).

Não temos um valor simples de ser interpretado como o \(R^{2}\) da Regressão Linear como antes. Para avaliar como o modelo está se saindo, precisamos ver a sua Matriz de Confusão.

Matriz de Confusão da Regressão Logística

A Matriz de Confusão é uma representação gráfica que nos permite visualizar de forma simples e rápida os erros e acertos do modelo (TP, TN, FP e FN). Para entender melhor a interpretação da matriz e as siglas, leia o nosso post Medidas de Performance: Modelos de Classificação.

Para podermos exibir a Matriz de Confusão, vamos precisar usar o método .predict() para termos as predições dos modelos armazenadas.

Vamos usar um Limiar de Classificação de 0.5. Tudo que tiver uma probabilidade de ser classe 1 maior que 0.5 vai ser classificado como tal. Todo o resto como classe 0.

# Realiza as predições na base de treino
# O limiar de classificação padrão é 0.5
pred_train = lg.predict(X_train) > 0.5
pred_train = np.round(pred_train)

# Gera a Matriz de Confusão
cm = confusion_matrix(y_train, pred_train)

# Plot da Matriz de Confusão
plt.figure(figsize=(7, 5))
sns.heatmap(cm, annot=True, fmt='g')
plt.title('Matriz de Confusão: Base de Treino', weight='bold')
plt.xlabel('Valores Previstos')
plt.ylabel('Valores Reais')
plt.show()

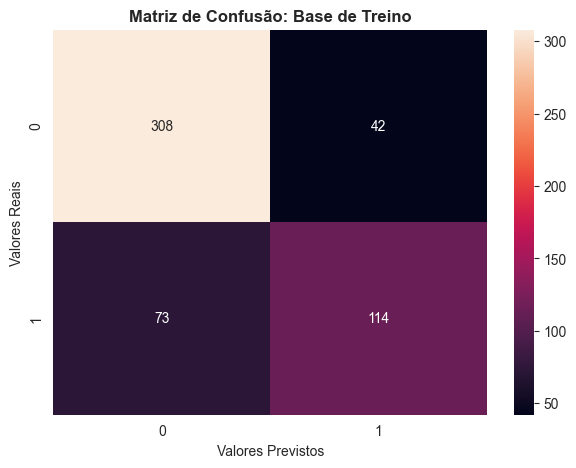
Observações

• Podemos ver que de 537 exemplos que temos na base de treino, acertamos 422.
• Precisamos dos quatro quadrantes para calcular nossas métricas. Foram 114 TPs, 308 TNs, 42 FPs e 73 FNs.

Com as informações da Matriz de Confusão, podemos verificar as métricas sobre nossa base de treino.

Métricas de Performance do Modelo

Vamos iremos avaliar as métricas de performance do modelo de classificação, como a Acurácia, Precisão e Recall.

# Acurácia
acc = accuracy_score(y_train, pred_train)
# Precisão
prec = precision_score(y_train, pred_train)
# Recall
rec = recall_score(y_train, pred_train)

print(f'Acurácia na base de treino: {round(acc, 2) * 100}%')
print(f'Precisão na base de treino: {round(prec, 2) * 100}%')
print(f'Recall na base de treino: {round(rec, 2) * 100}%')

E teremos a saída abaixo.

Acurácia na base de treino: 80.0%
Precisão na base de treino: 73.0%
Recall na base de treino: 61.0%

Conclusão sobre a prática de Regressão Logística

O modelo foi treinado com sucesso. A Acurácia nos diz que o nosso modelo consegue acertar em torno de 80% das predições. A Precisão, que quando o modelo classifica alguém como propenso à diabetes, ele acerta 73% das vezes. O Recall nos indica que o modelo detecta 61% dos diabéticos.

Perceba que o modelo teve foco maior em reduzir os FPs, de acordo com a métrica de Precisão maior que a de Recall.

O modelo está longe do ideal. Porém, em breve iremos ver modelos mais complexos e técnicas de como melhorar os resultados das classificações.

Devemos fazer a mesma avaliação acima para a base de teste, mas vou deixar para vocês fazerem essa etapa. Vamos encerrar por aqui esse laboratório de Regressão Logística.

Caso tenha ficado com alguma dúvida, entre em contato conosco!

Colabore com a nossa comunidade trazendo conteúdo de qualidade em Português, seja conteúdo próprio ou traduzido. Iremos ficar muito felizes de receber material de vocês.

Para conhecer mais sobre nós e saber como colaborar, visite o post abaixo.

• Bem-vindos ao BRAINS

É sempre um prazer estar com vocês por aqui!

#NoBrains #NoGains 🧠