Árvores de Decisão: Algoritmos Baseados em Árvores

Dois dos tipos de algoritmos mais avançados e eficientes que temos na atualidade são as Redes Neurais (Neural Networks), que estão dentro do campo de estudos do Deep Learning, e os algoritmos baseados em árvores (tree-based algorithms), como as Árvores de Decisão (ou Decision Trees) e suas variações.

Ultimamente o mercado e o mundo acadêmico têm dado muito foco ao Deep Learning e às Redes Neurais, mas de fato são as Árvores de Decisão que vêm ganhando boa parte das competições de Machine Learning e são definitivamente uma ferramenta extremamente útil e importante de termos na nossa oficina de Machine Learning.

Viemos falando sobre Machine Learning aqui no BRAINS, a nossa Brazilian AI Networks, há alguns posts. Para quem está iniciando no Machine Learning, recomendamos a leitura do post Primeiramente, o que é Machine Learning? Após este, uma boa leitura seria o Modelos de Classificação: Regressão Logística.

Mas, vamos lá!

O que são as Árvores de Decisão? 🌳

As Árvores de Decisão (Decision Trees) são um algoritmo não paramétrico de Aprendizado Supervisionado usado para Classificação e Regressão. É uma das técnicas mais usadas e eficientes para problemas de classificação que funciona muito bem com ambas, variáveis categóricas e contínuas.

Uma das formas mais fáceis de se entender uma Árvore de Decisão é através de uma representação gráfica. Tentamos cobrir todas as possíveis soluções para uma decisão que é baseada em uma certa condição. Neste algoritmo, os dados de treino são divididos em dois ou mais grupos baseados em condições de divisão sobre as variáveis de entrada.

Para ser mais didático, vamos analisar um exemplo retirado do material aberto da Carnegie Mellon University, School of Computer Science (SCS) sobre que tipo de lentes de contato uma pessoa deve utilizar (fonte: https://www.cs.cmu.edu/~bhiksha/courses/10-601/decisiontrees/).

Os tipos de lentes (classes), nossa variável alvo, são: nenhuma, rígidas e gelatinosas.

Os atributos (características) dos pacientes são: a taxa de produção de lágrimas (reduzida ou normal); se tem astigmatismo (sim ou não); faixa etária (se tem presbiopia ou não e se é jovem ou não); e a prescrição de óculos (miopia ou hipermetropia).

Baseados nestes atributos sobre os pacientes, conseguimos definir qual lente de contato o paciente deveria usar. Vamos construir nossa Árvore de Decisão e representá-la graficamente abaixo.

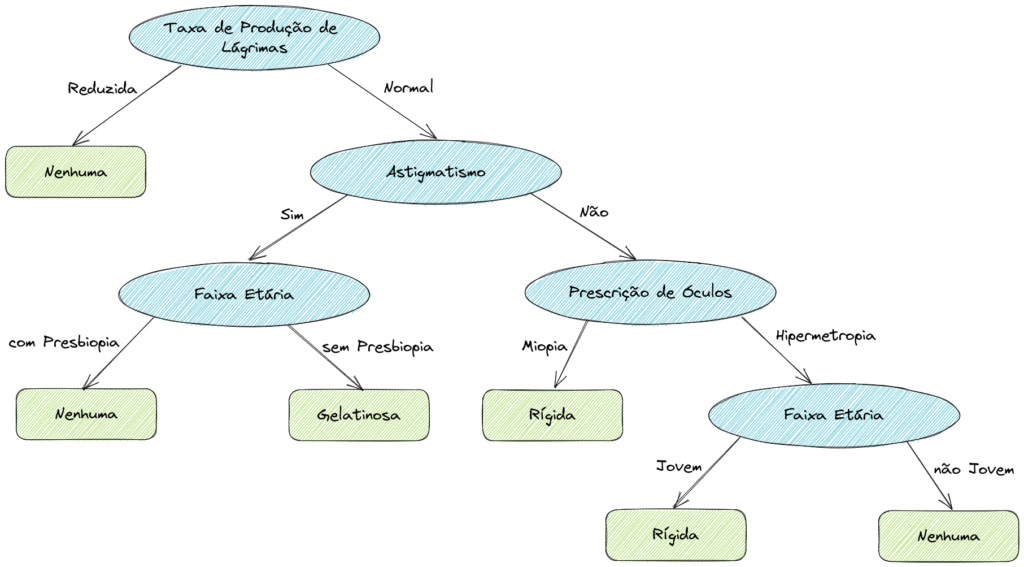
Não se parece muito com uma árvore, né? Provavelmente o nome vem de “árvores” da Ciência da Computação. As estruturas de dados baseadas em árvores possuem este mesmo formato representado acima no contexto da Ciência da Computação.

Vamos analisar algumas terminologias. Acredito que assim fará um pouco mais de sentido.

Terminologias das Árvores de Decisão

Cada forma geométrica da visualização acima é chamada de Nó (Node) em uma Árvore de Decisão. Nós temos diferentes tipos de Nós, dependendo em qual camada, ou profundidade, ele se encontra.

Vamos ver graficamente de novo.

Repare que temos dois tipos de formas geométricas, as arredondadas azuis e as retangulares verdes. Todos os nós que se dividem em “nós filhos” (dois ou mais nós subsequentes), são chamados de Nó de Decisão (Decision Node). Note que o primeiro Nó de Decisão tem um nome especial, é chamado de Nó Raiz (Root Node). Ambos estão representados como as formas arredondadas azuis.

Os nós finais, que não se dividem mais, são chamados de Nó Folha (Leaf Node), ou de Nó Terminal (Terminal Node). Estes são representados pelos retângulos verdes. E cada seta representando uma divisão é chamada de Galho (Branch).

Com essa nomenclatura fica mais fácil de assimilar a representação visual a uma árvore, certo? Uma árvore de cabeça para baixo, talvez.

Construindo Árvores de Decisão na prática

Para termos um exemplo um pouco mais próximo de uma aplicação de Machine Learning real, vamos simular a construção manual de uma Árvore de Decisão, na prática. Iremos falar de novo sobre o problema de classificação para detecção de e-mails Spam. Novamente, é um problema de Classificação Binária, onde precisamos que nosso modelo diga se um e-mail é provavelmente um Spam ou não. Duas classes apenas.

Para treino do nosso modelo, nós coletamos 10 exemplos de e-mails. Na base de treino temos dados sobre 3 características dos e-mails: Palavras-chave (se o e-mail contém palavras-chave típicas de um spam); Links Externos (se tem links externos com tentativa de phishing); Domínio (se é um domínio novo, recém cadastrado, ou antigo).

Como variável alvo, rotulada, a ser prevista pelo modelo, temos a coluna Spam. O valor 1 indica que o e-mail é um spam e 0 indica que não é. Temos 5 exemplos de cada uma destas duas classes.

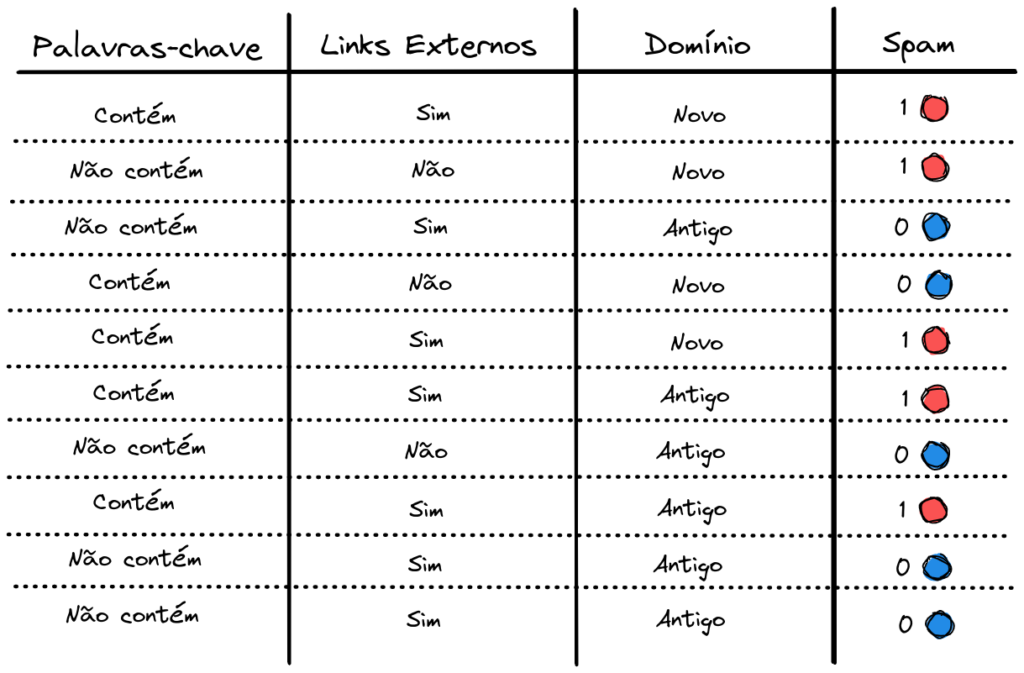
Temos todas as informações necessárias. Agora basta pegarmos cada um destes 3 atributos e fazer uma decisão em cima dele. Ou seja, iremos dividi-lo em galhos (ou ramificações) para tentar classificar nossos e-mails.

A nossa Árvore de Decisão ficaria da seguinte forma.

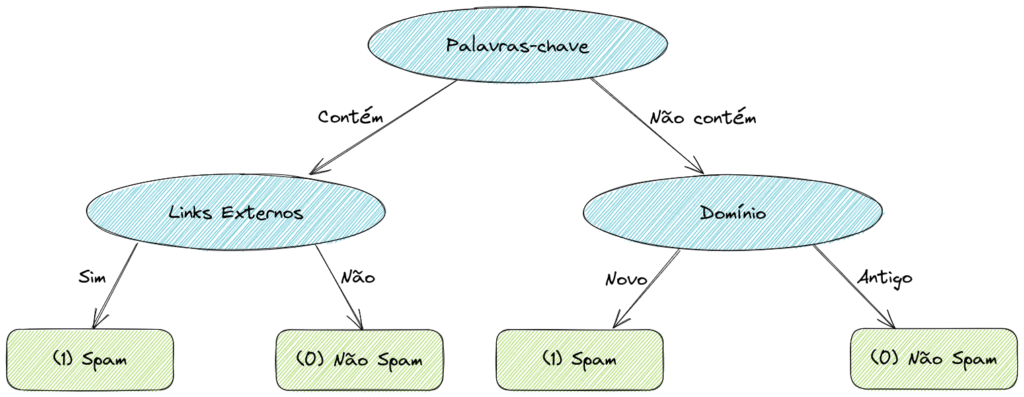
Aplicando sobre uma amostra

Vamos pegar um exemplo da nossa base de dados e ver como seria o processo de decisão da nossa árvore.

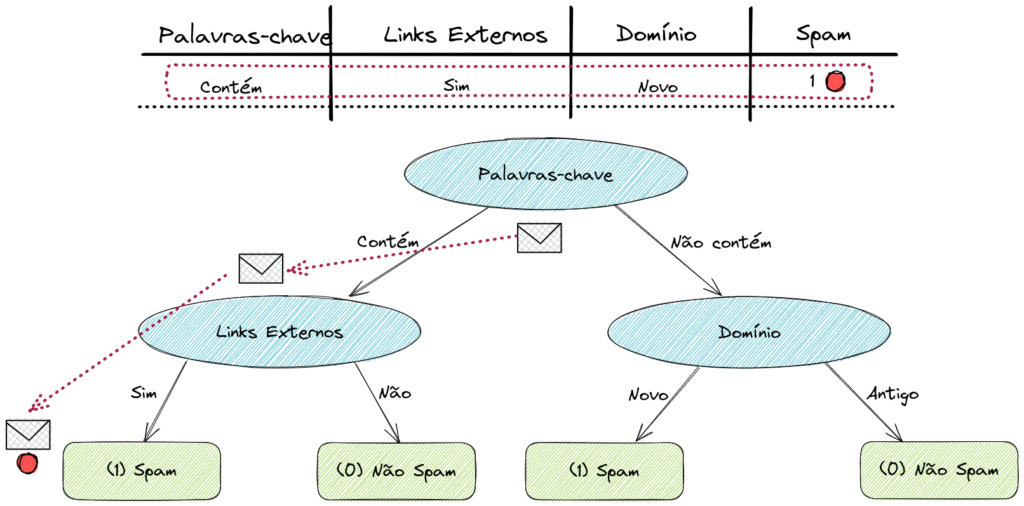
Fica bem fácil de acompanhar visualmente. A primeira decisão, do Nó Raiz (Root Node) é: o e-mail contém palavras-chave típicas de um spam? Se sim, seguimos o fluxo para a esquerda, se não, o fluxo para a direita.

Como na amostra que selecionamos o e-mail contém estas palavras, vamos para a esquerda e para o próximo Nó de Decisão (Decision Node). A decisão agora é: o e-mail possui links externos? Se sim, para a esquerda. Se não, para a direita.

Nesse exemplo, temos sim links externos, então seguimos o fluxo para a esquerda novamente. Chegamos assim, finalmente, a um Nó Folha (Leaf Node), também chamado de Nó Terminal (Terminal Node). Esse Nó Folha nos mostra que um e-mail com estas características deve ser classificado como spam.

Notou que, de forma simplificada, é uma sequência de condicionais if-else? E se você está se perguntando… sim, é daqui que saem os memes sobre Inteligência Artificial.

A melhor ordem das decisões

Se reparar bem, vai notar que essa Árvore de Decisão que construímos leva ao acerto de todos os exemplos da nossa base de dados. Isso a princípio é bom, temos uma performance excelente com dados de treino. Porém poderíamos ter diversas outras combinações de decisões, formando árvores diferentes.

Então com tantas opções e combinações diferentes, como chegamos à esta Árvore de Decisão ideal? Por que Links Externos ou Domínio não vieram primeiro como Nó Raiz? Por que essa árvore tem duas camadas de profundidade (dois níveis de decisão)? Para chegar a essas conclusões, precisamos entender o conceito de Impureza dos nossos dados.

Medidas de Impureza para Árvores de Decisão

Nosso problema a ser resolvido é uma Classificação Binária. Temos duas classes na nossa variável alvo, de interesse. Em todo o conjunto de dados, temos uma alta Impureza, pois de 10 exemplos, temos 5 de classe positiva (1, Spam) e 5 de classe negativa (0, Não Spam).

O cálculo de Impureza é bem simples e direto. Iremos analisar, dentre todos os exemplos disponíveis, quantos são da classe positiva e aplicar uma função sobre essa relação. Vamos iniciar calculando a relação de exemplos positivos versus todos os exemplos da nossa base de dados. Chamaremos essa relação de \(p_{1}\).

\[ p_{1} = \frac{\text{no. exemplos positivos}}{\text{no. exemplos totais}} \to \frac{5}{10} = 0.5\] \(0.5\) é a relação de maior Impureza possível. Temos exatamente metade dos dados como Classe Positiva (1) e metade dos dados como Classe Negativa (0). Um conjunto de dados 100% positivo ou 100% negativo é considerado um conjunto de dados Puro. E é isso que a Árvore de Decisão tenta encontrar.

Para buscar a pureza precisamos também, como falamos, aplicar uma função que nos auxilie a medir o nível de Impureza. Temos duas opções muito utilizadas: Entropia e Coeficiente de Gini.

O Coeficiente de Gini é uma medida de desigualdade (impureza; exatamente o que buscamos) desenvolvida pelo estatístico italiano Corrado Gini, e publicada no documento “Variabilità e mutabilità” (“Variabilidade e mutabilidade”, em italiano), em 1912.

Para fins de simplicidade e didática, vamos explorar aqui o cálculo de Entropia.

Entropia como medida de Impureza

A função de Entropia nos fornece o seguinte gráfico.

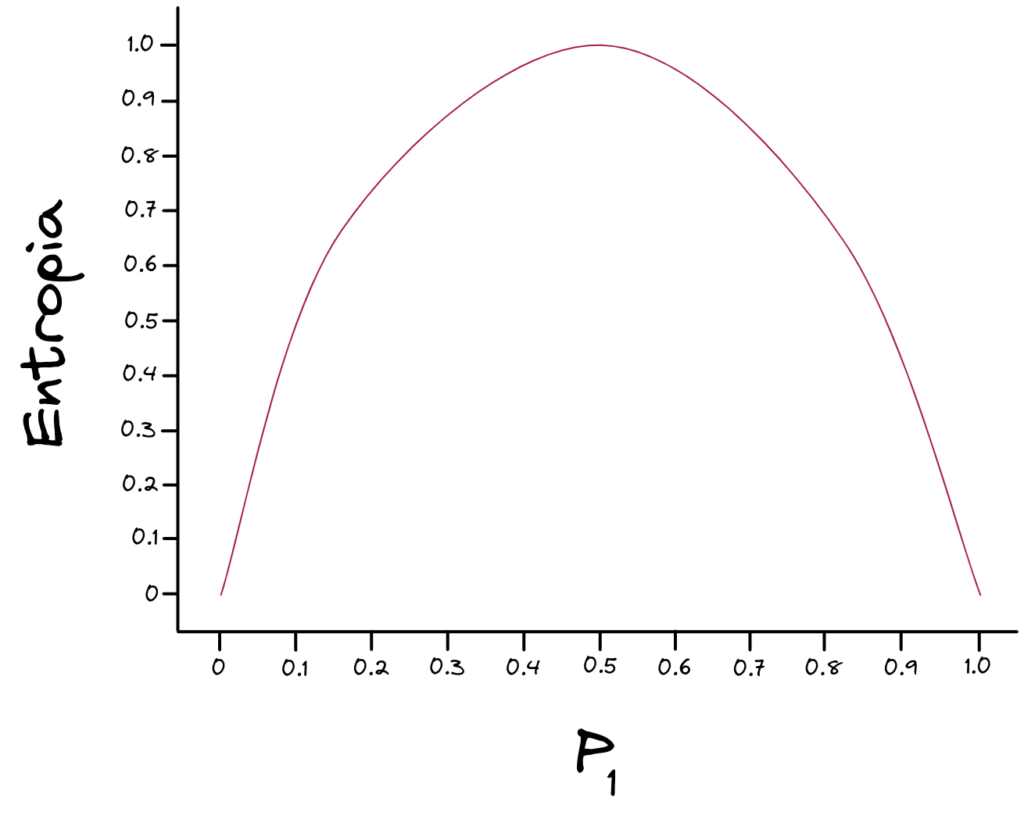
A função de Entropia – assim como o Coeficiente de Gini – começa no zero, sobe até o valor máximo de um, e volta para o zero. Uma função perfeita para ser aplicada no cálculo de Impureza. No eixo X, como entrada da função, temos a relação medida acima, \(p_{1}\).

Como dito, uma relação de 50/50 ( \(p_{1} = 0.5\) ) nos dá o valor mais alto de Impureza, que é uma Entropia de \(1\). Chamamos a função de Entropia de \(H\). Logo, temos o seguinte cálculo.

\[ H(p_{1}) = H(0.5) = 1.0 \]

Para os mais interessados na matemática, a fórmula exata da Entropia pode ser definida da forma abaixo.

\[ H(p_{1}) = -p_{1} \log_{2}(p_{1}) \ – (1 – p_{1}) \log_{2}(1 – p_{1}) \]

Se achou confuso, não se preocupe muito com a fórmula. O mais importante é entender que se não temos nenhum exemplo da classe positiva ( \(p_{1} = 0\) ) ou se todos os exemplos são da classe positiva ( \(p_{1} = 1.0\) ), temos pureza total, ou Entropia (impureza) igual a zero. Se temos metade dos exemplos de uma classe e metade da outra, temos o máximo de Entropia (impureza), que é o valor \(1.0\).

Entropia na prática

Vamos ver mais alguns exemplos para reforçar. Supondo que tenhamos 6 exemplos em um subconjunto de dados e que, destes temos 2 exemplos positivos apenas. Em um outro subconjunto também temos 6 exemplos e 5 exemplos positivos. Vamos calcular \(p_{1}\) nos dois casos.

\[ p_{1} = \frac{\text{no. exemplos positivos}}{\text{no. exemplos totais}} \to \frac{2}{6} = 0.33\]

\[ p_{1} = \frac{\text{no. exemplos positivos}}{\text{no. exemplos totais}} \to \frac{5}{6} = 0.83\]

E ao aplicarmos a função de Entropia, temos os seguintes resultados.

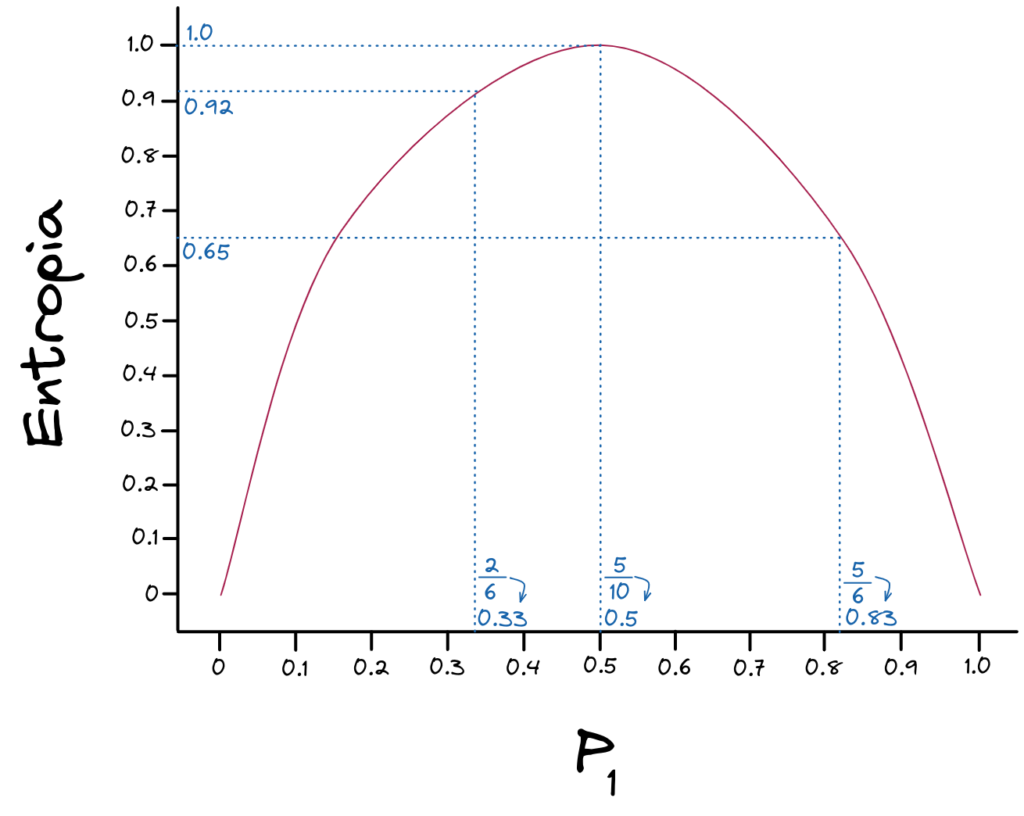
Podemos ver que aplicando a função de Entropia, teremos os seguintes resultados.

\[ p_{1} = \frac{5}{10} \to H(p_{1}) = 1.0 \]

\[ p_{1} = \frac{2}{6} \to H(p_{1}) = 0.92 \]

\[ p_{1} = \frac{5}{6} \to H(p_{1}) = 0.65 \]

Sabendo disso, podemos calcular quais divisões dos dados, ou decisões a serem tomadas, vão gerar uma saída mais pura, com um valor menor de Entropia (Impureza).

Nosso algoritmo irá buscar qual característica pode nos oferecer uma decisão (um if-else) que reduza ao máximo a Entropia/Impureza, ou que maximize a pureza dos dados após a decisão.

O termo usado nas Árvores de Decisão para essa redução de Impureza é chamado de Ganho de Informação (Information Gain).

Ganho de Informação: as melhores decisões

Como mencionamos, o algoritmo vai buscar as decisões que nos forneçam o maior Ganho de Informação. Em outras palavras, vamos buscar a divisão que vai nos dar dados mais puros, que vai reduzir ao máximo a Impureza.

Já sabemos como medir e calcular a Impureza por meio da Entropia (ou pelo Coeficiente de Gini). Portanto, basta testarmos a divisão em cada característica, medirmos a Entropia antes e depois desta divisão, e vermos o quanto de Entropia conseguimos reduzir. A Entropia antes menos a Entropia depois da divisão vai nos dar essa diferença, o Ganho de Informação (Information Gain).

Vamos ver com nosso exemplo prático de Spam como seria este cálculo. Vamos simular todas as decisões possíveis do nosso algoritmo.

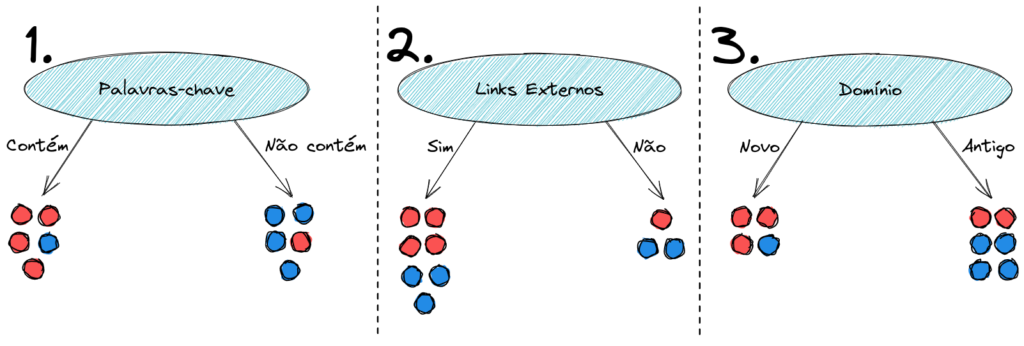
Para a primeira decisão da nossa árvore, o Nó Raiz, temos a opção de dividir em uma das três características. Vamos analisar uma a uma e calcular o ganho de informação em cada uma das opções.

Calculando o Ganho de Informação

Na primeira opção, decidindo sobre a característica Palavras-chave, temos as seguintes relações de \(p_{1}\) e Entropia.

\[ \begin{array}{cl}
p_{1} = \frac{4}{5} = 0.8 & \ & p_{1} = \frac{1}{5} = 0.2 \\
H(0.8) = 0.72 & \ & H(0.2) = 0.72
\end{array} \]

Após a divisão, nós temos dois subgrupos de dados, o da esquerda (Contém Palavras-chave) e o da direita (Não contém Palavras-chave). Precisamos encontrar a relação \(p_{1}\) e Entropia em cada uma dessas ramificações.

Em posse dos valores de Entropia das duas ramificações possíveis, precisamos tirar a média entre os dois valores. A média aritmética não seria uma medida justa porém, pois se um lado possui um enorme número de exemplos e está muito impuro, ele deveria ter um peso maior do que o lado que tem poucos exemplos e está mais puro.

A medida que leva em consideração esse peso dado à quantidade de exemplos é a Média Ponderada. Para calculá-la, basta multiplicar o valor da Entropia pela quantidade de exemplos disponíveis de cada lado.

\[ \left( \frac{5}{10} H(0.8) + \frac{5}{10} H(0.2) \right) \]

Sabemos que nessa primeira opção de divisão, por Palavras-chave, temos um total de 10 exemplos e 5 estão de cada lado da nossa divisão. Assim calculamos a Média Ponderada entre os dois valores de Entropia.

Para finalizar, como o Ganho de Informação é pedido pela diminuição da Entropia, precisamos subtrair do valor de Entropia antes da divisão essa média ponderada para verificar o quanto melhoramos. E sabemos que na nossa base de dados completa temos impureza máxima, de \(1.0\) ( \(p_{1} = 0.5\) ).

\[ H(0.5) \ – \left( \frac{5}{10} H(0.8) + \frac{5}{10} H(0.2) \right) = 0.28 \]

Com esta primeira opção, decidindo sobre a característica Palavras-chave, temos um Ganho de Informação de \(0.28\).

Verificando as outras características

Na segunda opção, decidindo sobre Links Externos, teremos os seguintes cálculos.

\[ \begin{array}{cl}
p_{1} = \frac{4}{7} = 0.57 & \ & p_{1} = \frac{1}{3} = 0.33 \\
H(0.57) = 0.99 & \ & H(0.33) = 0.92
\end{array} \]

\[ \left( \frac{7}{10} H(0.57) + \frac{3}{10} H(0.33) \right) \]

\[ H(0.5) \ – \left( \frac{7}{10} H(0.57) + \frac{3}{10} H(0.33) \right) = 0.03 \]

Portanto, para a divisão em Links Externos temos um Ganho de Informação de \(0.03\).

E, finalmente, para a terceira opção, decidindo sobre Domínio, os cálculos serão como abaixo.

\[ \begin{array}{cl}
p_{1} = \frac{3}{4} = 0.75 & \ & p_{1} = \frac{2}{6} = 0.33 \\
H(0.75) = 0.81 & \ & H(0.33) = 0.92
\end{array} \]

\[ \left( \frac{4}{10} H(0.75) + \frac{6}{10} H(0.33) \right) \]

\[ H(0.5) \ – \left( \frac{4}{10} H(0.57) + \frac{6}{10} H(0.33) \right) = 0.12 \]

Para a divisão em Domínio temos um Ganho de Informação de \(0.12\).

A melhor decisão

A melhor decisão a ser tomada será a que nos der um valor maior de Ganho de Informação. Neste caso, é a divisão pelo atributo Palavras-chave.

Para continuar construindo a Árvore de Decisão, iremos aplicar esse algoritmo de forma recursiva, construindo assim as próximas ramificações da mesma forma sobre os subconjuntos de dados gerados pela decisão anterior.

Variáveis Numéricas em Árvores de Decisão

Uma outra forma, muito interessante, de visualizar a Impureza e o Ganho de Informação é fazendo uso de variáveis contínuas (numéricas).

Vamos supor que temos uma base de dados com apenas duas características numéricas ( \(x_{1}\) e \(x_{2}\) ), para facilitar a visualização. E temos as duas classes diferentes neste espaço amostral: Spam e Não Spam.

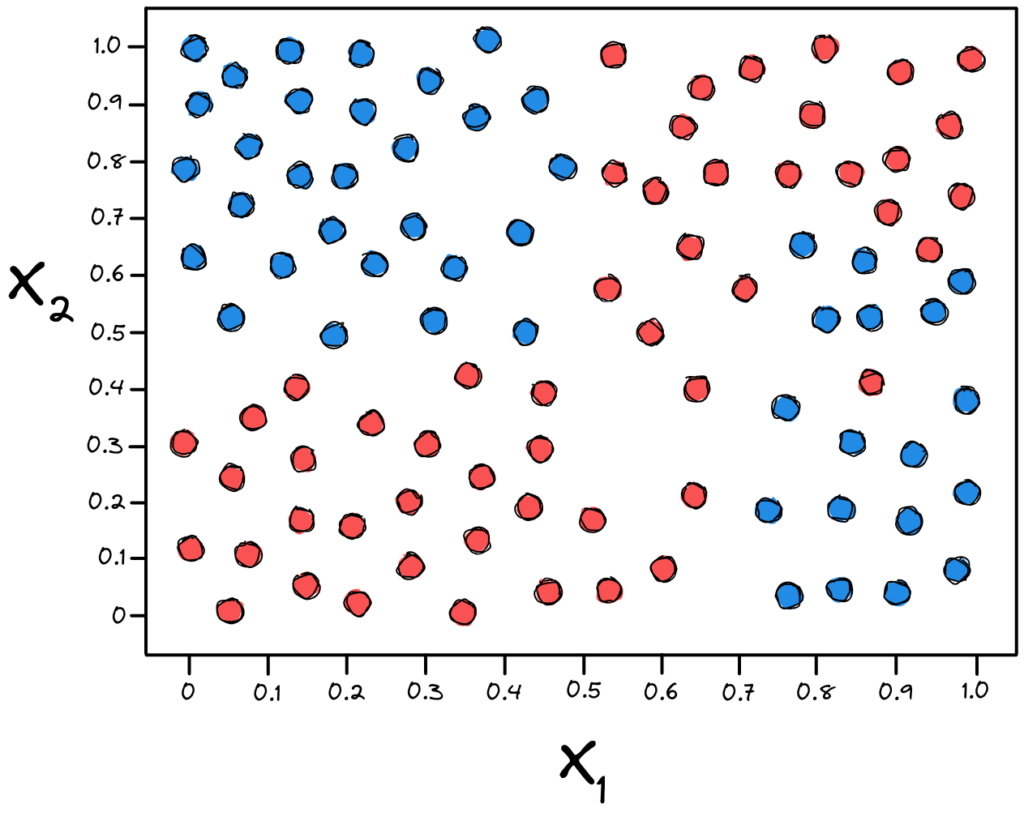
Para tomarmos decisões sobre variáveis numéricas e contínuas, precisamos definir limiares de “menor que” e “maior que”. Ou seja, vamos fazer cortes ortogonais (perfeitamente verticais ou perfeitamente horizontais) no nosso espaço amostral para dividir os nossos dados.

Novamente, o algoritmo irá buscar as divisões que nos apresentam um maior Ganho de Informação. Irá buscar decisões que deixem os dados mais puros após os cortes. A primeira decisão está representada pela linha roxa.

Podemos seguir fazendo novas decisões.

Se deixarmos, as Árvores de Decisão irão crescer até o seu limite, até ter 100% de pureza.

Neste último caso a Árvore de Decisão se adaptou 100% aos dados de treino, classificando todos corretamente. O que pode parecer bom, na verdade provavelmente se tornará um problema de Overfitting, onde o modelo se adapta demais aos dados de treino, “decorando” os resultados, mas falha miseravelmente em dados diferentes do de treino, como dados de Validação e Teste. Falaremos mais sobre isso em breve aqui no BRAINS.

Nós temos algumas formas de regularizar e controlar o tamanho das Árvores de Decisão. Nós chamamos esse controle das Árvores de Decisão de Poda (Prunning).

Poda das Árvores de Decisão

Nós temos duas formas de “podar” as nossas Árvores de Decisão: Pré-Poda (Pre-Prunning) e Pós-Poda (Post-Prunning). Ambas as técnicas têm como objetivo controlar o tamanho da Árvore de Decisão, evitando que elas se ajustem demais à base de treino, o que as levaria a falhar em dados novos – o que chamamos de problema de Overfitting.

As Árvores de Decisão podem crescer descontroladamente, ficando extremamente complexas e não conseguindo generalizar bem para novos dados, além dos dados de treino. Como analogia, podemos entender como que se a Árvore de Decisão “decorasse” os caminhos para acertar 100% da base de treino ao invés de capturar informações valiosas sobre os dados que possam ser generalizadas.

O processo de poda trata-se justamente de remover ramificações/galhos da árvore, reduzindo assim a sua complexidade. A Pré-Poda evita que a árvore cresça definindo alguns parâmetros. A Pós-Poda permite que ela cresça e depois é feita uma análise estatística de relevância para remover os galhos com menor significância.

Iremos aqui discutir brevemente a Pré-Poda (Pre-Prunning), de forma didática.

Pré-Poda: controlando o crescimento da árvore

Na biblioteca Open Source Scikit-Learn temos a classe DecisionTreeClassifier(). Esta classe nos permite configurar alguns Hiperparâmetros de regularização que irão controlar a complexidade das nossas Árvores de Decisão.

Um exemplo clássico e muito utilizado é o controle de profundidade da árvore. Ou seja, quantas camadas de Nós de Decisão iremos ter. Vamos ver abaixo alguns dos hiperparâmetros mais utilizados.

• max_depth \(\to\) profundidade máxima da árvore; quantas camadas de Nós de Decisão poderão ser criadas.
• max_features \(\to\) o número máximo de atributos/características avaliadas para divisão em cada nó.
• max_leaf_nodes \(\to\) número máximo de Nós Folha.
• min_samples_split \(\to\) número mínimo de exemplos que um nó precisa ter para ser subdividido.
• min_samples_leaf \(\to\) número mínimo de exemplos necessários para que um Nó Folha seja criado.
• min_weight_fraction_leaf \(\to\) o mesmo que acima, mas expressado como uma fração do total de exemplos com pesos diferentes.

Aumentar os hiperparâmetros min_* ou reduzir os max_* irá ajudar a regularizar o modelo. Ou seja, irá diminuir a complexidade e ajudar a criar um modelo que generalize melhor.

Estes são apenas alguns exemplos. A documentação será a sua melhor aliada nesse processo de criação do modelo ideal. Faz parte do trabalho de Machine Learning e Ciência de Dados analisar minuciosamente quais os parâmetros ideais para determinado modelo. 

Conclusão

As Árvores de Decisão são a base para alguns dos algoritmos mais eficientes de Machine Learning que temos acesso hoje. Alguns desses algoritmos são bem complexos e iremos falar sobre alguns deles em breve aqui no BRAINS.

Os algoritmos baseados em árvores são excelentes para se trabalhar com dados tabulares, também chamamos de dados estruturados.

Algumas vantagens são que as Árvores de Decisão são fáceis de entender e interpretar, o que dá uma alta transparência e explicabilidade para o modelo. São muito úteis para exploração de dados, pois nos indica a significância (ou relevância) das variáveis. Não são tão influenciadas por Outliers e valores nulos, e não precisamos assumir certas premissas sobre os dados, o que nos poupa um pouco de tempo na preparação da base de treino. Elas conseguem também lidar com variáveis categóricas e contínuas.

Uma das maiores desvantagens são que uma pequena alteração na base de treino pode resultar em uma enorme alteração na estrutura da Árvore de Decisão, o que gera instabilidade do modelo. Iremos ver em breve como resolver esse problema, em um outro post.

Outra desvantagem é que o modelo tende ao Overfitting. Conseguimos ver formas de evitar isso com a poda das árvores, mas é sempre importante manter esta tendência em mente.

Espero que tenha gostado deste post. Em breve falaremos mais sobre algoritmos baseados em árvores por aqui pelo BRAINS. Iremos demonstrar também como construir Árvores de Decisão na prática, usando o Python.

Se você ficou com alguma dúvida, ficaremos felizes em ajudar pelos comentários. E se você tem interesse em colaborar com a nossa comunidade, entre em contato com a gente.

Todos são bem-vindos a colaborar! Não importa o seu nível de conhecimento. Para saber mais sobre a nossa comunidade, visite o nosso post BRAINS – Brazilian AI Networks.

#NoBrains #NoGains 🧠