Estamos em uma sequência de posts sobre Large Language Models – os enormes modelos de linguagem e IA Generativa – e explorando conceitos super importantes para entender como esses modelos funcionam e como podemos fazer o melhor uso possível deles. Um dos grandes poderes de se trabalhar com os modelos de Processamento de Linguagem Natural é manipular o que chamamos de Embeddings. E hoje vamos explorar um pouco mais sobre este tema.
Se você não sabe exatamente o que são os Embeddings, o que são Tokens, como são formados e para que servem, recomendo a leitura do post Token e Embedding: conceitos da IA e LLMs. Caso queira dar mais um passo para trás, pode ler também um post mais introdutório, o Introdução aos LLMs e à IA Generativa.
Para os mais avançados, que querem explorar de fato a arquitetura de Transformers e o Mecanismo de Atenção, recomendo o Os Transformers Ilustrados.
Mas vamos lá, vamos entender um pouco melhor como podemos, matematicamente, medir a distância, e consequentemente, a similaridade entre dois Embeddings.
Recapitulando, o que são Embeddings?
Nós já vimos anteriormente, neste post, o que são os Embeddings, como são formados e para que servem. E como definimos, o Embedding é a representação vetorial de um texto em um espaço multidimensional. Ou seja, um modelo (ou uma camada) de Embeddings vai transformar texto em vetores. E por texto, a gente pode entender como um único Token, uma palavra, ou grandes quantidades de sentenças. Todo pedaço de texto pode ser convertido em Embeddings.
Aprendemos também que Embeddings similares tendem a se agrupar. Palavras ou textos semelhantes, vão ficar próximos nesse espaço vetorial. O modelo irá, com sua inteligência artificial, aprender a separar os textos. E irá tender a deixar coisas parecidas próximas e coisas muito diferentes distantes.
Para exemplificar, vamos pegar um exemplo com algumas palavras e em um plano de duas dimensões. Teremos neste exemplo, alguns animais, móveis de uma casa, dinheiro e frutas. O modelo irá posicionar cada uma dessas palavras em uma posição com coordenadas no plano bidimensional.
Repare que palavras similares, tendem a se agrupar. São pontos com coordenadas próximas. Ou vetores similares, para sermos mais exatos.
E quando esse modelo recebe uma palavra nova, como "abacaxi", ele sabe exatamente onde colocar. Muito provavelmente na região onde estão outras frutas.
Vamos agora começar a estudar a relação entre esses pontos, ou esses Embeddings.
Embeddings são Álgebra Linear pura
Nós, apesar de definirmos os Embeddings como “representação vetorial”, não estamos os representando visualmente como vetores. E vocês devem se lembrar que cálculos com Vetores são uma matéria da Álgebra Linear. Vamos relembrar alguns conceitos.
Um Vetor, na Ciência da Computação, pode ser definido como um array de números. Ou como uma Matrix de uma só coluna. Em Python, a biblioteca mais utilizada para trabalhar com vetores é a NumPy.
Os vetores também podem ser representados como setas em um plano, ou em um espaço de maiores dimensões, como um Hiperplano. Dois componentes super importantes dos vetores são a sua Magnitude, ou o seu tamanho, e a sua Direção.
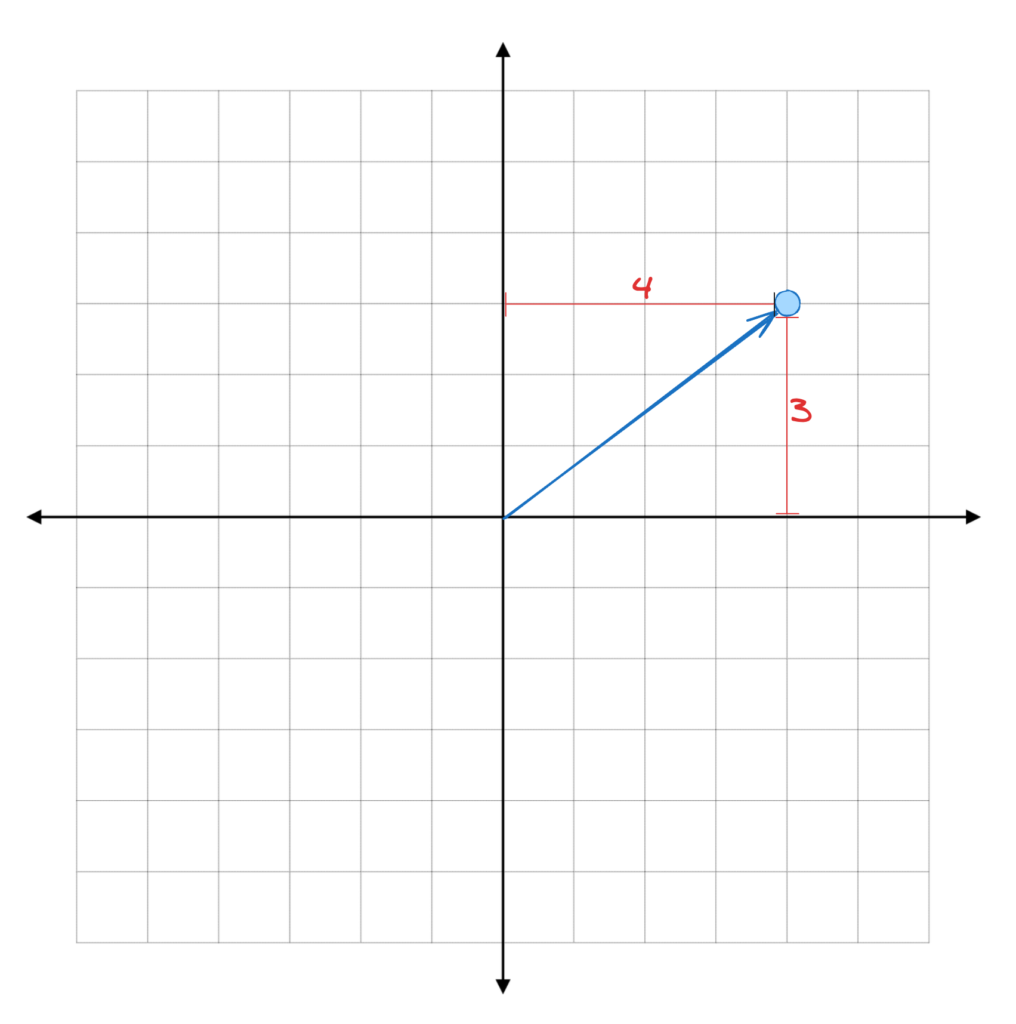
Como vimos anteriormente, essas setas podem ser representadas como uma sequência de números. Ou como coordenadas. O número de coordenadas que um Embedding tem é o número de dimensões do espaço vetorial onde ele se encontra. Por exemplo, um vetor com as coordenadas (4, 3) se encontra em um plano 2D, bidimensional, e a sua seta parte da Origem (0, 0) e se encerra exatamente no ponto com a coordenada horizontal 4 e a coordenada vertical 3.
Nós podemos ter vetores com mais dimensões, como por exemplo em 3D. O vetor com coordenadas (4, 3, 1) possui três dimensões e, portanto, mora em um espaço tridimensional. Este vetor também parte da origem (0, 0, 0) e se encerra nas coordenadas horizontal x = 4, vertical y = 3 e de profundidade z = 1.
Direção dos Vetores
A Direção de um vetor pode ser encontrada a partir das suas coordenadas. Por exemplo, esse vetor com coordenadas (4, 3), dado que o ângulo entre ele e o eixo horizontal é Theta \((\theta)\), então a Tangente de Theta \((\tan \theta )\) é precisamente \(\frac{3}{4}\).

Isso significa que Theta \((\theta)\) é o Arco Tangente (ou Tangente Inversa) de \(\frac{3}{4}\), que é \(36.87\) graus. Ou, caso prefiram, \(0.64\) radianos.
A conta seria feita da seguinte forma.
\[ \tan(\theta) = \frac{3}{4} \]
\[ \theta = \arctan \left( \frac{3}{4} \right) = 0.64 \text{ rad} = 36.87 \text{ graus} \]
Magnitude dos Vetores
A Magnitude, ou tamanho, dos vetores podem ser definidos de diversas formas. A boa notícia é que todas elas também se baseiam nas coordenadas do vetor e emulam distâncias que nós utilizados na vida real. Afinal de contas, a Magnitude do vetor é a distância da Origem até a coordenada final do vetor.
Norma L1: a Distância do Táxi 🚕
A primeira forma de medir distância é: imagine que você vive em uma cidade formada por quadras quadradas com ruas totalmente perpendiculares. Temos ruas verticais e horizontais, todas de mão dupla. E a única forma de se locomover nessa cidade é pelas ruas, de Táxi, por exemplo.
Portanto, para sairmos da Origem (0, 0) e chegarmos à coordenada final do nosso Vetor (4, 3), precisamos andar 4 quadras horizontais e 3 quadras verticais. Portanto, a nossa distância total é de 4 + 3 = 7. Andamos 7 quadras unidades de medida para chegar no final do nosso vetor.

E o interessante é que não importa o caminho que tomarmos. Se dermos passos horizontais e verticais em direção à coordenada final do vetor, sempre vamos chegar ao valor de distância de 7.

Esta medida de distância é conhecida como Norma L1, ou a Distância do Táxi. E quando medimos esta distância da Origem (0, 0) até a coordenada final do Vetor (a, b), temos exatamente a soma dos valores absolutos (em módulo) de \(a\) e \(b\).
Por que os valores absolutos? Porque os valores das coordenadas \(a\) e \(b\) podem ser positivos ou negativos. Mas a distância é sempre positiva.
\[ \text{Norma L1} = |(a, \ b)|_1 = |a| + |b| \]
E esta Norma L1 é chamada também em algumas literaturas como a Distância de Manhattan. Isso acontece porque a cidade de Manhattan, em Nova Iorque, segue mais ou menos esse formato de quadras com ruas perpendiculares. Por isso deram este nome também para essa medida de distância.

Norma L2: a Distância Euclidiana, do Helicóptero 🚁
Para uma segunda forma de medir distância, imagine que nesta mesma cidade, em todas as esquinas existe um heliponto. E que você pode simplesmente pegar um helicóptero e viajar em linha reta até onde quer chegar.
Neste caso, para sairmos da Origem (0, 0) e chegarmos ao final do nosso Vetor (4, 3), nós podemos pegar a Hipotenusa, ou seja, a linha reta entre os dois pontos deste plano.
O melhor caminho que podemos fazer é a raiz quadrada de \(4^2\) mais \(3^2\) \((\sqrt{4^2 + 3^2})\), que é precisamente igual a \(5\).
Isso acontece por conta do Teorema de Pitágoras, que afirma que “a Hipotenusa de um Triângulo Retângulo é igual à raiz quadrada da soma dos quadrados dos catetos”. Ou seja, o maior lado do Triângulo Retângulo é igual à raiz quadrada da soma dos outros dois lados elevados ao quadrado.

Esta medida de distância é conhecida como Norma L2, ou a Distância Euclidiana – o helicóptero aqui foi ilustrativo. E quando medimos esta distância da Origem (0, 0) até a coordenada final do Vetor (a, b), temos exatamente o cálculo da hipotenusa. Ou seja, a raiz quadrada da soma dos quadrados das coordenadas.
\[ \text{Norma L2} = |(a, \ b)|_2 = \sqrt{a^2 + b^2} \]
E desenvolvendo o cálculo, temos:
\[ |(4, \ 3)|_2 = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5\]
Nós sabemos que a menor distância entre dois pontos vai ser sempre uma linha reta. Portanto, a Norma L2, ou Distância Euclidiana, vai ser sempre menor (ou igual) à Norma L1.
Similaridade de Embeddings
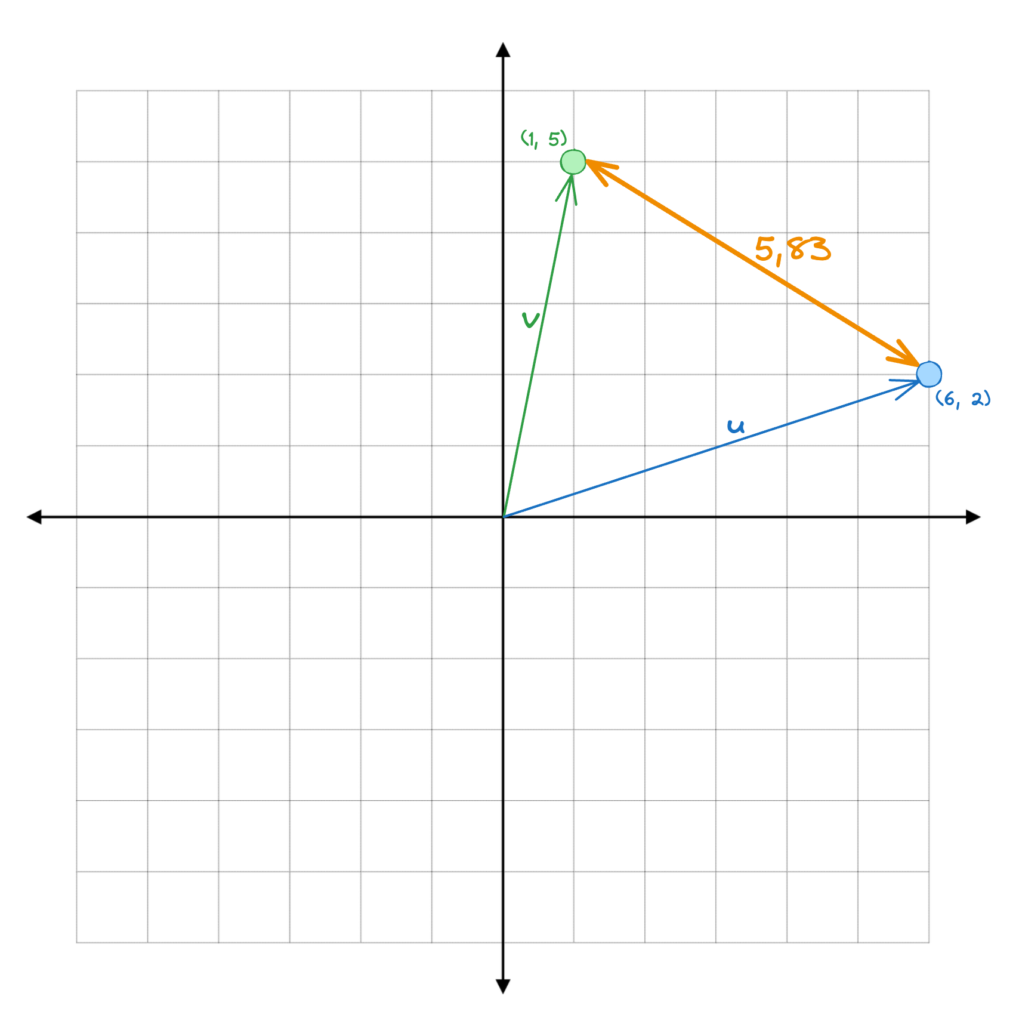
Vimos como medir a Magnitude dos Embeddings, ou Vetores. Ou seja, a distância da Origem até a coordenada final do vetor. Mas e a distância entre dois Embeddings? Por exemplo, qual a diferença entre o vetor (1, 5) e o vetor (6, 2)?

Já sabemos que quanto mais semelhantes/similares os Embeddings são, mais próximos eles ficam. Portanto, quanto menor a distância entre dois Embeddings, maior a tendência de os textos originais serem semanticamente parecidos. Concordam?
A primeira maneira de medir a distância entre estes dois Embeddings, ou Vetores, é usando a Norma L1 que acabamos de ver. Ela vai ser a soma dos valores absolutos dos componentes, que é igual a 8.
\[ \text{Norma L1} \longrightarrow |(u, \ v)|_1 = |1 – 6| + |5 – 2| \]
\[ |(u, \ v)|_1 = |5| + |-3| \]
Que nos dá o valor final:
\[ |(u, \ v)|_1 = 8 \]
Podemos comprovar visualmente o resultado.

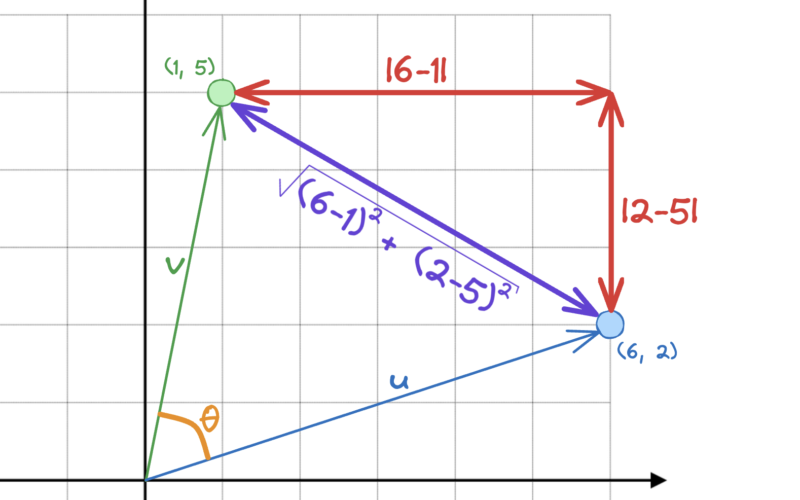
Outra maneira de medir a similaridade destes dois Embeddings é, obviamente, usando a Distância Euclidiana, ou a Norma L2 desta diferença. Ao aplicarmos o Teorema de Pitágoras, onde consideramos \(v\) e \(u\) como lados de um triângulo retângulo, encontramos que a hipotenusa é igual a \(5.83\).
\[ \text{Norma L2} \longrightarrow |(u, \ v)|_2 = \sqrt{(1 – 6)^2 + (5 – 2)^2} \]
\[ |(u, \ v)|_2 = \sqrt{(5)^2 + (-3)^2} = \sqrt{34} \]
Resultando em uma distância final de:
\[ |(u, \ v)|_2 = 5.83 \]
Novamente, conseguimos visualizar graficamente.
Norma L1 vs Norma L2: quando usar cada uma?
Bom, cada caso é um caso, e as aplicações devem ser exploradas individualmente. Mas vamos analisar conceitualmente as diferenças entre essas duas medidas de similaridade de Embeddings para entender onde uma pode ter vantagem sobre a outra.
Benefícios da Norma L1 para Embeddings
A Norma L1 é geralmente mais robusta e menos sensível aos Outliers, do que a Norma L2. Isso quer dizer que a Norma L1 é menos afetada por valores extremos. E o motivo é óbvio, dado que a Norma L2 trabalha com valores ao quadrado, o que aumenta o peso dos outliers exponencialmente. Como a Norma L1 apenas extrai o valor absoluto, lida com o peso dos outliers de forma linear.
Em tarefas de classificação de texto, em muitas dimensões e com features esparsas (como em modelos Bag-of-Words), a Norma L1 pode ser bastante eficaz. Por exemplo, ao classificar documentos com base na ocorrência de palavras-chave, a Norma L1 pode lidar melhor com a “esparsidade” e fornecer medições de distância mais significativas entre os documentos.
Na análise de sentimentos, onde o espaço de recursos pode incluir outliers (como palavras com pontuações de sentimento extremamente altas ou baixas), a Norma L1 pode ser mais robusta. É menos sensível a valores extremos, que podem representar palavras raras, mas intensamente sentimentais, garantindo que esses outliers não afetem desproporcionalmente o cálculo do sentimento geral.
Benefícios da Norma L2 para Embeddings
Entretanto, a Norma L2 leva muito mais em consideração a Magnitude dos Embeddings, o que carrega consigo mais informação semântica e contextual.
Ao usar embeddings de palavras como Word2Vec ou GloVe para tarefas de similaridade semântica, a Norma L2 pode ser mais eficaz. Nestes casos, a magnitude dos vetores de embedding muitas vezes carrega informações semânticas importantes. Por exemplo, ao agrupar palavras semelhantes com base em suas representações vetoriais, a Distância Euclidiana (Norma L2) pode refletir com mais precisão as distâncias semânticas, levando a um melhor agrupamento de palavras semanticamente similares.
Por padrão, quando não especificamos qual Norma utilizar, nós assumimos que estamos usando a Norma L2. Isso acontece inclusive com boa parte das bibliotecas Python. O motivo é que esta é uma forma mais natural de se medir distância. Até porque é exatamente o comprimento da seta, a magnitude do Vetor.
Distância de Cosseno ⦨
A Distância de Cosseno, também chamada de Similaridade de Cosseno, é também uma métrica de similaridade de Embeddings muito popular no Processamento de Linguagem Natural. Diferente das Normas L1 e L2, a Similaridade de Cosseno mede o cosseno do ângulo entre os dois vetores, independente da Magnitude deles. Nesse caso, apenas a direção dos Embeddings é relevante.
Vamos chamar o ângulo entre os dois vetores de Theta \((\theta)\). A Distância de Cosseno é simplesmente o cosseno de Theta \((\cos (\theta))\).

A Similaridade de Cosseno é particularmente útil como medida de similaridade em Embeddings de palavras (tipo Word2Vec e GloVe). Essa medida captura a orientação – ou direção – dos vetores, que é normalmente mais importante que a sua magnitude quando se fala de relação entre palavras.
Para similaridade de documentos, quando representamos documentos como vetores (como vetores TF-IDF), a Distância de Cosseno consegue medir o quão similares os documentos são com base nos seus conteúdos, independente do tamanho.
Enquanto as Normas L1 e L2 são úteis em cenários onde a magnitude dos vetores é importante, como em clusterizações, onde a distância de fato é importante, a Similaridade de Cosseno é mais aplicada em casos em que a direção do vetor é mais relevante, como medir a similaridade semântica entre documentos.
Em resumo, a Distância de Cosseno é a medida preferida em tarefas de NLP (Natural Language Processing) onde a direção dos vetores é mais importante que as suas magnitudes.
Conclusão
Como falamos, a melhor medida de distância (e similaridade) vai depender especificamente do caso de uso em questão. Vale a pena analisar cada caso e experimentar com as diferentes medidas. Nós vimos aqui apenas três formas de medir a similaridade entre Embeddings. Porém há muitas outras medidas de distância, como a medida de Hamming, Minkowski, Chebyshev, Jaccard e outras.
Outro ponto importante é que Embeddings realistas vão ter muito mais do que 2 dimensões. O mais normal atualmente são Embeddings que têm entre 512 a 4096 dimensões, ou seja, 512 a 4096 coordenadas finais para cada vetor. Nós não conseguimos visualizar mais do que três dimensões, portanto mantivemos apenas duas para fins didáticos. Vale a pena ler o post Token e Embedding: conceitos da IA e LLMs para entender melhor como isso funciona. Independente da quantidade de dimensões, os cálculos são os mesmos.
Nós podemos também sair do campo dos Hiper Planos e trabalhar com Hiper Esferas. Mas estes temas são assunto para um próximo post. Comente aqui caso queira que falemos mais sobre essas outras formas de medir similaridade entre os Embeddings.
Deixe nos comentários também se você gostou deste conteúdo, ou se não gostou também. Nos avise caso tenha ficado com dúvidas ou se quiser complementar o tema.
Não se esqueça que todos são bem-vindos a contribuir com o BRAINS. Seja por meio de conteúdo próprio, resumo dos seus estudos, ou até traduções de conteúdos gringos (com a devida permissão dos autores). Todo conteúdo de qualidade em Português será muito bem-vindo por aqui.
Para ficar por dentro dos próximos posts, sigam a nossa página no LinkedIn. E para conhecer um pouco mais sobre a nossa comunidade, leia o post de introdução ao BRAINS – Brazilian AI Networks.
E lembre-se…




2 comentários
André, bom dia. Tudo bem?
Estou com uma dúvida: no texto temos que “as Normas L1 e L2 são úteis em cenários onde a magnitude dos vetores é importante, como em clusterizações, onde a distância de fato é importante, a Similaridade de Cosseno é mais aplicada em casos em que a direção do vetor é mais relevante, como medir a similaridade semântica entre documentos”.
Pensando em uma clusterização de texto pela similaridade semântica, poderíamos combinar estas duas medidas? Faz sentido usar isso?
A pergunta foi feita pensado que Similaridade de Cosseno daria a direção mas os textos podem estar em posições distantes por causa do tamanho da norma do vetor. a combinação poderia dar um resultado melhor na clusterização?
Fala Rodrigo! Tudo ótimo por aqui, e contigo?
Cara, é uma excelente pergunta! Intrigante. Mas como você faria? Tipo um Stacking de modelos? Pensando alto aqui, pegar o top 10 mais similares por L2 e o top 10 mais similares com Cosseno, e ver 5 que sejam comuns aos dois? E pegar o top 5 comum aos dois?
Seria algo assim? Vamos conversar mais sobre isso!